98 Bernoulli’s Equation
Learning Objectives
By the end of this section, you will be able to:
- Explain the terms in Bernoulli’s equation.
- Explain how Bernoulli’s equation is related to conservation of energy.
- Explain how to derive Bernoulli’s principle from Bernoulli’s equation.
- Calculate with Bernoulli’s principle.
- List some applications of Bernoulli’s principle.
When a fluid flows into a narrower channel, its speed increases. That means its kinetic energy also increases. Where does that change in kinetic energy come from? The increased kinetic energy comes from the net work done on the fluid to push it into the channel and the work done on the fluid by the gravitational force, if the fluid changes vertical position. Recall the work-energy theorem,
There is a pressure difference when the channel narrows. This pressure difference results in a net force on the fluid: recall that pressure times area equals force. The net work done increases the fluid’s kinetic energy. As a result, the pressure will drop in a rapidly-moving fluid, whether or not the fluid is confined to a tube.
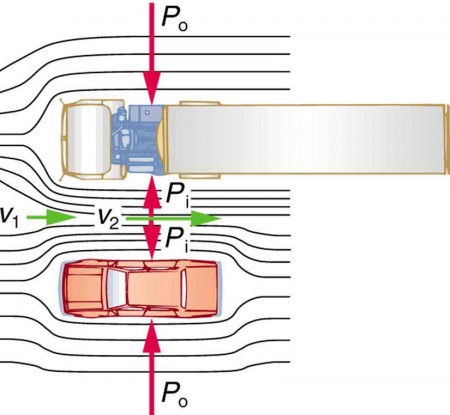
There are a number of common examples of pressure dropping in rapidly-moving fluids. Shower curtains have a disagreeable habit of bulging into the shower stall when the shower is on. The high-velocity stream of water and air creates a region of lower pressure inside the shower, and standard atmospheric pressure on the other side. The pressure difference results in a net force inward pushing the curtain in. You may also have noticed that when passing a truck on the highway, your car tends to veer toward it. The reason is the same—the high velocity of the air between the car and the truck creates a region of lower pressure, and the vehicles are pushed together by greater pressure on the outside. (See Figure 1.) This effect was observed as far back as the mid-1800s, when it was found that trains passing in opposite directions tipped precariously toward one another.
Making Connections: Take-Home Investigation with a Sheet of Paper
Bernoulli’s Equation
The relationship between pressure and velocity in fluids is described quantitatively by Bernoulli’s equation, named after its discoverer, the Swiss scientist Daniel Bernoulli (1700–1782). Bernoulli’s equation states that for an incompressible, frictionless fluid, the following sum is constant:
[latex]P+\frac{1}{2}\rho v^{2}+\rho gh=\text{constant}\\[/latex],
where P is the absolute pressure, ρ is the fluid density, v is the velocity of the fluid, h is the height above some reference point, and g is the acceleration due to gravity. If we follow a small volume of fluid along its path, various quantities in the sum may change, but the total remains constant. Let the subscripts 1 and 2 refer to any two points along the path that the bit of fluid follows; Bernoulli’s equation becomes
[latex]{P}_{1}+\frac{1}{2}{{\rho v}_{1}}^{2}+\rho {gh}_{1}={P}_{2}+\frac{1}{2}{{\rho v}_{2}}^{2}+\rho {gh}_{2}\\[/latex].
Bernoulli’s equation is a form of the conservation of energy principle. Note that the second and third terms are the kinetic and potential energy with m replaced by ρ. In fact, each term in the equation has units of energy per unit volume. We can prove this for the second term by substituting ρ = m/V into it and gathering terms:
[latex]\frac{1}{2}{\rho v}^{2}=\frac{\frac{1}{2}{\text{mv}}^{2}}{V}=\frac{\text{KE}}{V}\\[/latex]
So [latex]\frac{1}{2}{\rho v}^{2}\\[/latex] is the kinetic energy per unit volume. Making the same substitution into the third term in the equation, we find
[latex]\rho {gh}=\frac{mgh}{V}=\frac{{\text{PE}}_{\text{g}}}{V}\\[/latex],
so ρgh is the gravitational potential energy per unit volume. Note that pressure P has units of energy per unit volume, too. Since P = F/A, its units are N/m2. If we multiply these by m/m, we obtain N ⋅ m/m3 = J/m3, or energy per unit volume. Bernoulli’s equation is, in fact, just a convenient statement of conservation of energy for an incompressible fluid in the absence of friction.
Making Connections: Conservation of Energy
The general form of Bernoulli’s equation has three terms in it, and it is broadly applicable. To understand it better, we will look at a number of specific situations that simplify and illustrate its use and meaning.
Bernoulli’s Equation for Static Fluids
Let us first consider the very simple situation where the fluid is static—that is, v1 = v2 = 0. Bernoulli’s equation in that case is
P1 + ρgh1 = P2 + ρgh2.
We can further simplify the equation by taking h2 = 0 (we can always choose some height to be zero, just as we often have done for other situations involving the gravitational force, and take all other heights to be relative to this). In that case, we get
[latex]{P}_{2}={P}_{1}+\rho {gh}_{1}\\[/latex]
This equation tells us that, in static fluids, pressure increases with depth. As we go from point 1 to point 2 in the fluid, the depth increases by h1, and consequently, P2 is greater than P1 by an amount ρgh1. In the very simplest case, P1 is zero at the top of the fluid, and we get the familiar relationship P = ρgh. (Recall that P = ρgh and [latex]\Delta{\text{PE}}_{\text{g}}= mgh\\[/latex]) Bernoulli’s equation includes the fact that the pressure due to the weight of a fluid is ρgh. Although we introduce Bernoulli’s equation for fluid flow, it includes much of what we studied for static fluids in the preceding chapter.
Bernoulli’s Principle—Bernoulli’s Equation at Constant Depth
Another important situation is one in which the fluid moves but its depth is constant—that is, h1 = h2. Under that condition, Bernoulli’s equation becomes
[latex]{P}_{1}+\frac{1}{2}{{\rho v}_{1}}^{2}={P}_{2}+\frac{1}{2}{{\rho v}_{2}}^{2}\\[/latex].
Situations in which fluid flows at a constant depth are so important that this equation is often called Bernoulli’s principle. It is Bernoulli’s equation for fluids at constant depth. (Note again that this applies to a small volume of fluid as we follow it along its path.) As we have just discussed, pressure drops as speed increases in a moving fluid. We can see this from Bernoulli’s principle. For example, if v2 is greater than v1 in the equation, then P2 must be less than P1 for the equality to hold.
Example 1. Calculating Pressure: Pressure Drops as a Fluid Speeds Up
In Example 1 from Flow Rate and Its Relation to Velocity, we found that the speed of water in a hose increased from 1.96 m/s to 25.5 m/s going from the hose to the nozzle. Calculate the pressure in the hose, given that the absolute pressure in the nozzle is 1.0 × 105 N/m2 (atmospheric, as it must be) and assuming level, frictionless flow.
Strategy
Level flow means constant depth, so Bernoulli’s principle applies. We use the subscript 1 for values in the hose and 2 for those in the nozzle. We are thus asked to find P1.
Solution
Solving Bernoulli’s principle for P1 yields
[latex]{P}_{1}={P}_{2}+\frac{1}{2}{{\rho v}_{2}}^{2}-\frac{1}{2}{{\rho v}_{1}}^{2}={P}_{2}+\frac{1}{2}\rho \left({{v}_{2}}^{2}-{{v}_{1}}^{2}\right)\\[/latex]
Substituting known values,
[latex]\begin{array}{c}{P}_{1} = 7 1.01\times 10^{5} \text{ N/m}^{2} +\frac{1}{2}\left(10^{3}\text{ kg/m}^{3}\right)\left[\left(25.5 \text{ m/s}\right)^{2}-\left(1.96 \text{ m/s}\right)^{2}\right]\\ = 4.24\times {10}^{5}\text{ N/m}^{2}\end{array}\\[/latex]
Discussion
This absolute pressure in the hose is greater than in the nozzle, as expected since v is greater in the nozzle. The pressure P2 in the nozzle must be atmospheric since it emerges into the atmosphere without other changes in conditions.
Applications of Bernoulli’s Principle
There are a number of devices and situations in which fluid flows at a constant height and, thus, can be analyzed with Bernoulli’s principle.
Entrainment
People have long put the Bernoulli principle to work by using reduced pressure in high-velocity fluids to move things about. With a higher pressure on the outside, the high-velocity fluid forces other fluids into the stream. This process is called entrainment. Entrainment devices have been in use since ancient times, particularly as pumps to raise water small heights, as in draining swamps, fields, or other low-lying areas. Some other devices that use the concept of entrainment are shown in Figure 2.

Wings and Sails
The airplane wing is a beautiful example of Bernoulli’s principle in action. Figure 2(a) shows the characteristic shape of a wing. The wing is tilted upward at a small angle and the upper surface is longer, causing air to flow faster over it. The pressure on top of the wing is therefore reduced, creating a net upward force or lift. (Wings can also gain lift by pushing air downward, utilizing the conservation of momentum principle. The deflected air molecules result in an upward force on the wing — Newton’s third law.) Sails also have the characteristic shape of a wing. (See Figure 2(b).) The pressure on the front side of the sail, Pfront, is lower than the pressure on the back of the sail, Pback. This results in a forward force and even allows you to sail into the wind.
Making Connections: Take-Home Investigation with Two Strips of Paper
Velocity measurement
Figure 3 shows two devices that measure fluid velocity based on Bernoulli’s principle. The manometer in Figure 3(a) is connected to two tubes that are small enough not to appreciably disturb the flow. The tube facing the oncoming fluid creates a dead spot having zero velocity (v1=0) in front of it, while fluid passing the other tube has velocity v2. This means that Bernoulli’s principle as stated in [latex]{P}_{1}+\frac{1}{2}{{\rho v}_{1}}^{2}={P}_{2}+\frac{1}{2}{{\rho v}_{2}}^{2}\\[/latex] becomes [latex]{P}_{1}={P}_{2}+\frac{1}{2}{{\rho v}_{2}}^{2}\\[/latex].

Thus pressure P2 over the second opening is reduced by [latex]\frac{1}{2}{{\rho v}_{2}}^{2}\\[/latex], and so the fluid in the manometer rises by h on the side connected to the second opening, where
[latex]h\propto \frac{1}{2}{{\rho v}_{2}}^{2}\\[/latex]
(Recall that the symbol ∝ means “proportional to.”) Solving for v2, we see that
[latex]{v}_{2}\propto \sqrt{h}\\[/latex].
Figure 4(b) shows a version of this device that is in common use for measuring various fluid velocities; such devices are frequently used as air speed indicators in aircraft.

Section Summary
- Bernoulli’s equation states that the sum on each side of the following equation is constant, or the same at any two points in an incompressible frictionless fluid:
[latex]{P}_{1}+\frac{1}{2}{{\rho v}_{1}}^{2}+\rho {gh}_{1}={P}_{2}+\frac{1}{2}{{\rho v}_{2}}^{2}+\rho {gh}_{2}\\[/latex].
- Bernoulli’s principle is Bernoulli’s equation applied to situations in which depth is constant. The terms involving depth (or height h) subtract out, yielding
[latex]{P}_{1}+\frac{1}{2}{{\rho v}_{1}}^{2}={P}_{2}+\frac{1}{2}{{\rho v}_{2}}^{2}\\[/latex].
- Bernoulli’s principle has many applications, including entrainment, wings and sails, and velocity measurement.
Conceptual Questions
1. You can squirt water a considerably greater distance by placing your thumb over the end of a garden hose and then releasing, than by leaving it completely uncovered. Explain how this works.
2. Water is shot nearly vertically upward in a decorative fountain and the stream is observed to broaden as it rises. Conversely, a stream of water falling straight down from a faucet narrows. Explain why, and discuss whether surface tension enhances or reduces the effect in each case.
3. Refer to Figure 1. Answer the following two questions. Why is Po less than atmospheric? Why is Po greater than Pi ?

4. Give an example of entrainment not mentioned in the text.
5. Many entrainment devices have a constriction, called a Venturi, such as shown in Figure 5. How does this bolster entrainment?

6. Some chimney pipes have a T-shape, with a crosspiece on top that helps draw up gases whenever there is even a slight breeze. Explain how this works in terms of Bernoulli’s principle.
7. Is there a limit to the height to which an entrainment device can raise a fluid? Explain your answer.
8. Why is it preferable for airplanes to take off into the wind rather than with the wind?
9. Roofs are sometimes pushed off vertically during a tropical cyclone, and buildings sometimes explode outward when hit by a tornado. Use Bernoulli’s principle to explain these phenomena.
10. Why does a sailboat need a keel?
11. It is dangerous to stand close to railroad tracks when a rapidly moving commuter train passes. Explain why atmospheric pressure would push you toward the moving train.
12. Water pressure inside a hose nozzle can be less than atmospheric pressure due to the Bernoulli effect. Explain in terms of energy how the water can emerge from the nozzle against the opposing atmospheric pressure.
13. A perfume bottle or atomizer sprays a fluid that is in the bottle. (Figure 6.) How does the fluid rise up in the vertical tube in the bottle?

14. If you lower the window on a car while moving, an empty plastic bag can sometimes fly out the window. Why does this happen?
Problems & Exercises
1. Verify that pressure has units of energy per unit volume.
2. Suppose you have a wind speed gauge like the pitot tube shown in Example 2 from Flow Rate and Its Relation to Velocity. By what factor must wind speed increase to double the value of h in the manometer? Is this independent of the moving fluid and the fluid in the manometer?
3. If the pressure reading of your pitot tube is 15.0 mm Hg at a speed of 200 km/h, what will it be at 700 km/h at the same altitude?
4. Calculate the maximum height to which water could be squirted with the hose in Example 2 from Flow Rate and Its Relation to Velocity if it: (a) Emerges from the nozzle. (b) Emerges with the nozzle removed, assuming the same flow rate.
5. Every few years, winds in Boulder, Colorado, attain sustained speeds of 45.0 m/s (about 100 mi/h) when the jet stream descends during early spring. Approximately what is the force due to the Bernoulli effect on a roof having an area of 220 m2? Typical air density in Boulder is 1.14 kg/m3, and the corresponding atmospheric pressure is 8.89 × 104 N/m2. (Bernoulli’s principle as stated in the text assumes laminar flow. Using the principle here produces only an approximate result, because there is significant turbulence.)
6. (a) Calculate the approximate force on a square meter of sail, given the horizontal velocity of the wind is 6.00 m/s parallel to its front surface and 3.50 m/s along its back surface. Take the density of air to be 1.29 kg/m3. (The calculation, based on Bernoulli’s principle, is approximate due to the effects of turbulence.) (b) Discuss whether this force is great enough to be effective for propelling a sailboat.
7. (a) What is the pressure drop due to the Bernoulli effect as water goes into a 3.00-cm-diameter nozzle from a 9.00-cm-diameter fire hose while carrying a flow of 40.0 L/s? (b) To what maximum height above the nozzle can this water rise? (The actual height will be significantly smaller due to air resistance.)
8. (a) Using Bernoulli’s equation, show that the measured fluid speed v for a pitot tube, like the one in Figure 4(b), is given by
[latex]v={\left(\frac{2\rho′gh}{\rho }\right)}^{1/2}\\[/latex],
where h is the height of the manometer fluid,
[latex]\rho′\\[/latex] is the density of the manometer fluid, [latex]\rho\\[/latex] is the density of the moving fluid, and g is the acceleration due to gravity. (Note that v is indeed proportional to the square root of h, as stated in the text.) (b) Calculate v for moving air if a mercury manometer’s h is 0.200 m.
Glossary
- Bernoulli’s equation:
- the equation resulting from applying conservation of energy to an incompressible frictionless fluid: P + 1/2pv2 + pgh = constant , through the fluid
- Bernoulli’s principle:
- Bernoulli’s equation applied at constant depth: P1 + 1/2pv12 = P2 + 1/2pv22
Selected Solutions to Problems & Exercises
1. [latex]\begin{array}{c} {P}&=&\frac{\text{Force}}{\text{Area}}, \\ (P)_{\text{units}}&=&\text{N/m}^{2}=\text{N}\cdot\text{m/m}^{3}=\text{J/m}^{3}\\ &=& \text{energy/volume}\end{array}\\[/latex]
3. 184 mm Hg
5. 2.54 × 105 N
7. (a) 1.58 × 106 N/m2 (b) 163 m

