116 Phase Change and Latent Heat

Learning Objectives

By the end of this section, you will be able to:

  • Examine heat transfer.
  • Calculate final temperature from heat transfer.

So far we have discussed temperature change due to heat transfer. No temperature change occurs from heat transfer if ice melts and becomes liquid water (i.e., during a phase change). For example, consider water dripping from icicles melting on a roof warmed by the Sun. Conversely, water freezes in an ice tray cooled by lower-temperature surroundings.

The given figure shows a vertically downward, knife-shaped ice piece, with water droplets sparkling on its surface.
Figure 1. Heat from the air transfers to the ice causing it to melt. (credit: Mike Brand)

Energy is required to melt a solid because the cohesive bonds between the molecules in the solid must be broken apart such that, in the liquid, the molecules can move around at comparable kinetic energies; thus, there is no rise in temperature. Similarly, energy is needed to vaporize a liquid, because molecules in a liquid interact with each other via attractive forces. There is no temperature change until a phase change is complete. The temperature of a cup of soda initially at 0ºC stays at 0ºC until all the ice has melted. Conversely, energy is released during freezing and condensation, usually in the form of thermal energy. Work is done by cohesive forces when molecules are brought together. The corresponding energy must be given off (dissipated) to allow them to stay together Figure 2.

The energy involved in a phase change depends on two major factors: the number and strength of bonds or force pairs. The number of bonds is proportional to the number of molecules and thus to the mass of the sample. The strength of forces depends on the type of molecules. The heat Q required to change the phase of a sample of mass m is given by

Q = mLf (melting/freezing,

Q = mLv (vaporization/condensation),

where the latent heat of fusion, Lf, and latent heat of vaporization, Lv, are material constants that are determined experimentally. See (Table 1).

Figure a shows a four by four square lattice object labeled solid. The lattice is made of four rows of red spheres, with each row containing four spheres. The spheres are attached together horizontally and vertically by springs, defining vacant square spaces between the springs. A short arrow points radially outward from each sphere. The arrows on the different spheres point in different directions but are the same length, and one of them terminates at a dashed circle that is labeled limits of motion. To the right of this object are shown two curved arrows. The upper curved arrow points rightward and is labeled “energy input” and “melt.” The lower arrow points leftward and is labeled “energy output” and “freeze.” To the right of the curved arrows is a drawing labeled liquid. This drawing contains nine red spheres arranged randomly, with a curved arrow emanating from each sphere. The arrows are of different lengths and point in different directions.Figure b shows a drawing labeled liquid that is essentially the same as that of figure a. To the right of this drawing are shown two curved arrows. The upper curved arrow points rightward and is labeled “energy input” and “boil.” The lower arrow points leftward and is labeled “energy output” and “condense.” To the right of the curved arrows is another drawing of randomly arranged red spheres that is labeled gas. This drawing contains eight red spheres and each sphere has a straight or a curved arrow emanating from it. Compared to the drawing to the left that is labeled liquid, these arrows are longer and the red spheres are more widely spaced.
Figure 2. (a) Energy is required to partially overcome the attractive forces between molecules in a solid to form a liquid. That same energy must be removed for freezing to take place. (b) Molecules are separated by large distances when going from liquid to vapor, requiring significant energy to overcome molecular attraction. The same energy must be removed for condensation to take place. There is no temperature change until a phase change is complete.

Latent heat is measured in units of J/kg. Both Lf and Lv depend on the substance, particularly on the strength of its molecular forces as noted earlier. Lf and Lv are collectively called latent heat coefficients. They are latent, or hidden, because in phase changes, energy enters or leaves a system without causing a temperature change in the system; so, in effect, the energy is hidden. Table 1 lists representative values of Lf and Lv, together with melting and boiling points.

The table shows that significant amounts of energy are involved in phase changes. Let us look, for example, at how much energy is needed to melt a kilogram of ice at 0ºC to produce a kilogram of water at 0°C. Using the equation for a change in temperature and the value for water from Table 1, we find that Q = mLf = (1.0 kg)(334 kJ/kg) = 334 kJ is the energy to melt a kilogram of ice. This is a lot of energy as it represents the same amount of energy needed to raise the temperature of 1 kg of liquid water from 0ºC to 79.8ºC. Even more energy is required to vaporize water; it would take 2256 kJ to change 1 kg of liquid water at the normal boiling point (100ºC at atmospheric pressure) to steam (water vapor). This example shows that the energy for a phase change is enormous compared to energy associated with temperature changes without a phase change.

Table 1. Heats of Fusion and Vaporization[1]
Lf Lv
Substance Melting point (ºC) kJ/kg kcal/kg Boiling point (°C) kJ/kg kcal/kg
Helium −269.7 5.23 1.25 −268.9 20.9 4.99
Hydrogen −259.3 58.6 14.0 −252.9 452 108
Nitrogen −210.0 25.5 6.09 −195.8 201 48.0
Oxygen −218.8 13.8 3.30 −183.0 213 50.9
Ethanol −114 104 24.9 78.3 854 204
Ammonia −75 108 −33.4 1370 327
Mercury −38.9 11.8 2.82 357 272 65.0
Water 0.00 334 79.8 100.0 2256[2] 539[3]
Sulfur 119 38.1 9.10 444.6 326 77.9
Lead 327 24.5 5.85 1750 871 208
Antimony 631 165 39.4 1440 561 134
Aluminum 660 380 90 2450 11400 2720
Silver 961 88.3 21.1 2193 2336 558
Gold 1063 64.5 15.4 2660 1578 377
Copper 1083 134 32.0 2595 5069 1211
Uranium 1133 84 20 3900 1900 454
Tungsten 3410 184 44 5900 4810 1150

Phase changes can have a tremendous stabilizing effect even on temperatures that are not near the melting and boiling points, because evaporation and condensation (conversion of a gas into a liquid state) occur even at temperatures below the boiling point. Take, for example, the fact that air temperatures in humid climates rarely go above 35.0ºC, which is because most heat transfer goes into evaporating water into the air. Similarly, temperatures in humid weather rarely fall below the dew point because enormous heat is released when water vapor condenses.

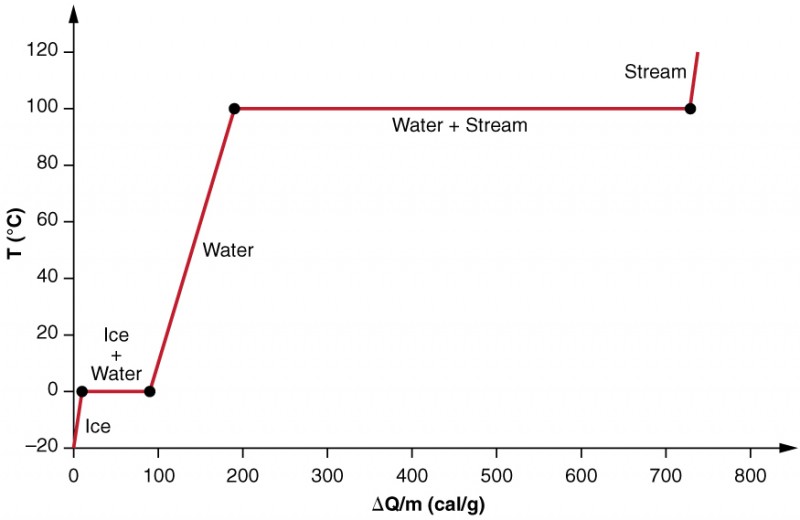
We examine the effects of phase change more precisely by considering adding heat into a sample of ice at −20ºC (Figure 3). The temperature of the ice rises linearly, absorbing heat at a constant rate of 0.50 cal/g⋅ºC until it reaches 0ºC. Once at this temperature, the ice begins to melt until all the ice has melted, absorbing 79.8 cal/g of heat. The temperature remains constant at 0ºC during this phase change. Once all the ice has melted, the temperature of the liquid water rises, absorbing heat at a new constant rate of 1.00 cal/g⋅ºC. At 100ºC, the water begins to boil and the temperature again remains constant while the water absorbs 539 cal/g of heat during this phase change. When all the liquid has become steam vapor, the temperature rises again, absorbing heat at a rate of 0.482 cal/g⋅ºC.

The figure shows a two-dimensional graph with temperature plotted on the vertical axis from minus twenty to one hundred and twenty degrees Celsius. The horizontal axis is labeled delta Q divided by m and, in parentheses, calories per gram. This horizontal axis goes from zero to eight hundred. A line segment labeled ice extends upward and rightward at about 60 degrees above the horizontal from the point minus twenty degrees Celsius, zero delta Q per m to the point zero degrees Celsius and about 40 delta Q per m. A horizontal line segment labeled ice and water extends rightward from this point to approximately 120 delta Q per m. A line segment labeled water then extends up and to the right at approximately 70 degrees above the horizontal to the point one hundred degrees Celsius and about 200 delta Q per m. From this latter point a horizontal line segment labeled water plus steam extends to the right to about 780 delta Q per m. From here, a final line segment labeled steam extends up and to the right at about 60 degrees above the horizontal to about one hundred and twenty degrees Celsius and 800 delta Q per m.
Figure 3. A graph of temperature versus energy added. The system is constructed so that no vapor evaporates while ice warms to become liquid water, and so that, when vaporization occurs, the vapor remains in of the system. The long stretches of constant temperature values at 0ºC and 100ºC reflect the large latent heat of melting and vaporization, respectively.

Water can evaporate at temperatures below the boiling point. More energy is required than at the boiling point, because the kinetic energy of water molecules at temperatures below 100ºC is less than that at 100ºC, hence less energy is available from random thermal motions. Take, for example, the fact that, at body temperature, perspiration from the skin requires a heat input of 2428 kJ/kg, which is about 10 percent higher than the latent heat of vaporization at 100ºC. This heat comes from the skin, and thus provides an effective cooling mechanism in hot weather. High humidity inhibits evaporation, so that body temperature might rise, leaving unevaporated sweat on your brow.

Example 1. Calculate Final Temperature from Phase Change: Cooling Soda with Ice Cubes

Three ice cubes are used to chill a soda at 20ºC with mass msoda = 0.25 kg. The ice is at 0ºC and each ice cube has a mass of 6.0 g. Assume that the soda is kept in a foam container so that heat loss can be ignored. Assume the soda has the same heat capacity as water. Find the final temperature when all ice has melted.

Strategy

The ice cubes are at the melting temperature of 0ºC. Heat is transferred from the soda to the ice for melting. Melting of ice occurs in two steps: first the phase change occurs and solid (ice) transforms into liquid water at the melting temperature, then the temperature of this water rises. Melting yields water at 0ºC, so more heat is transferred from the soda to this water until the water plus soda system reaches thermal equilibrium, Qice = − Qsoda.

The heat transferred to the ice is

Qice = mice Lf + micecW(Tf−0ºC).

The heat given off by the soda is Qsoda = msodacW(Tf−20ºC). Since no heat is lost, Qice = −Qsoda, so that

mice Lf + micecW(Tf−0ºC) = –msodacW(Tf−20ºC).

Bring all terms involving Tf on the left-hand-side and all other terms on the right-hand-side. Solve for the unknown quantity Tf:

[latex]\displaystyle{T}_{\text{f}}=\frac{m_{\text{soda}}c_{\text{W}}\left(20^{\circ}\text{C}\right)-m_{\text{ice}}L_{\text{f}}}{\left(m_{\text{soda}}+m_{\text{ice}}\right)c_{\text{W}}}\\[/latex]

Solution

  1. Identify the known quantities. The mass of ice is mice = 3 × 6.0 g = 0.018 kg and the mass of soda is msoda = 0.25 kg.
  2. Calculate the terms in the numerator: m sodacW(20ºC)=(0.25 kg)(4186 J/kg ⋅ ºC)(20ºC) = 20,930 J and miceLf = (0.018 kg)(334,000 J/kg) = 6012 J.
  3. Calculate the denominator: (msoda + mice)cW = (0.25 kg + 0.018 kg)(4186 K/(kg⋅ºC) = 1122 J/ºC.
  4. Calculate the final temperature: [latex]\displaystyle{T}_{\text{f}}=\frac{20,930\text{ J}-6012\text{ J}}{1122\text{ J/}^{\circ}\text{C}}=13^{\circ}\text{C}\\[/latex]

Discussion

This example illustrates the enormous energies involved during a phase change. The mass of ice is about 7 percent the mass of water but leads to a noticeable change in the temperature of soda. Although we assumed that the ice was at the freezing temperature, this is incorrect: the typical temperature is −6ºC. However, this correction gives a final temperature that is essentially identical to the result we found. Can you explain why?

The figure shows condensed water droplets on a glass of iced tea.
Figure 4. Condensation on a glass of iced tea. (credit: Jenny Downing)

We have seen that vaporization requires heat transfer to a liquid from the surroundings, so that energy is released by the surroundings. Condensation is the reverse process, increasing the temperature of the surroundings. This increase may seem surprising, since we associate condensation with cold objects—the glass in the figure, for example. However, energy must be removed from the condensing molecules to make a vapor condense. The energy is exactly the same as that required to make the phase change in the other direction, from liquid to vapor, and so it can be calculated from Q = mLv.

Condensation forms in Figure 4 because the temperature of the nearby air is reduced to below the dew point. The air cannot hold as much water as it did at room temperature, and so water condenses. Energy is released when the water condenses, speeding the melting of the ice in the glass.

Real-World Application

Energy is also released when a liquid freezes. This phenomenon is used by fruit growers in Florida to protect oranges when the temperature is close to the freezing point (0ºC). Growers spray water on the plants in orchards so that the water freezes and heat is released to the growing oranges on the trees. This prevents the temperature inside the orange from dropping below freezing, which would damage the fruit.

The figure shows bare tree branches covered with ice and icicles.
Figure 14.11. The ice on these trees released large amounts of energy when it froze, helping to prevent the temperature of the trees from dropping below 0ºC. Water is intentionally sprayed on orchards to help prevent hard frosts. (credit: Hermann Hammer)

Sublimation is the transition from solid to vapor phase. You may have noticed that snow can disappear into thin air without a trace of liquid water, or the disappearance of ice cubes in a freezer. The reverse is also true: Frost can form on very cold windows without going through the liquid stage. A popular effect is the making of “smoke” from dry ice, which is solid carbon dioxide. Sublimation occurs because the equilibrium vapor pressure of solids is not zero. Certain air fresheners use the sublimation of a solid to inject a perfume into the room. Moth balls are a slightly toxic example of a phenol (an organic compound) that sublimates, while some solids, such as osmium tetroxide, are so toxic that they must be kept in sealed containers to prevent human exposure to their sublimation-produced vapors.

Figure a shows vapors flowing out from the middle of three glasses placed adjacently on a table. This glass contains a piece of dry ice in lemonade. Two squeezed lemon slices are also seen alongside the glasses. Figure b shows frost patterns formed on a window pane.
Figure 5. Direct transitions between solid and vapor are common, sometimes useful, and even beautiful. (a) Dry ice sublimates directly to carbon dioxide gas. The visible vapor is made of water droplets. (credit: Windell Oskay) (b) Frost forms patterns on a very cold window, an example of a solid formed directly from a vapor. (credit: Liz West)

All phase transitions involve heat. In the case of direct solid-vapor transitions, the energy required is given by the equation Q = mLs, where Ls is the heat of sublimation, which is the energy required to change 1.00 kg of a substance from the solid phase to the vapor phase. Ls is analogous to Lf and Lv, and its value depends on the substance. Sublimation requires energy input, so that dry ice is an effective coolant, whereas the reverse process (i.e., frosting) releases energy. The amount of energy required for sublimation is of the same order of magnitude as that for other phase transitions.

The material presented in this section and the preceding section allows us to calculate any number of effects related to temperature and phase change. In each case, it is necessary to identify which temperature and phase changes are taking place and then to apply the appropriate equation. Keep in mind that heat transfer and work can cause both temperature and phase changes.

Problem-Solving Strategies for the Effects of Heat Transfer

  1. Examine the situation to determine that there is a change in the temperature or phase. Is there heat transfer into or out of the system? When the presence or absence of a phase change is not obvious, you may wish to first solve the problem as if there were no phase changes, and examine the temperature change obtained. If it is sufficient to take you past a boiling or melting point, you should then go back and do the problem in steps—temperature change, phase change, subsequent temperature change, and so on.
  2. Identify and list all objects that change temperature and phase.
  3. Identify exactly what needs to be determined in the problem (identify the unknowns). A written list is useful.
  4. Make a list of what is given or what can be inferred from the problem as stated (identify the knowns).
  5. Solve the appropriate equation for the quantity to be determined (the unknown). If there is a temperature change, the transferred heat depends on the specific heat (see Table 1 in Temperature Change and Heat Capacity) whereas, for a phase change, the transferred heat depends on the latent heat. See Table 1.
  6. Substitute the knowns along with their units into the appropriate equation and obtain numerical solutions complete with units. You will need to do this in steps if there is more than one stage to the process (such as a temperature change followed by a phase change).
  7. Check the answer to see if it is reasonable: Does it make sense? As an example, be certain that the temperature change does not also cause a phase change that you have not taken into account.

Check Your Understanding

Why does snow remain on mountain slopes even when daytime temperatures are higher than the freezing temperature?

Solution

Snow is formed from ice crystals and thus is the solid phase of water. Because enormous heat is necessary for phase changes, it takes a certain amount of time for this heat to be accumulated from the air, even if the air is above 0ºC. The warmer the air is, the faster this heat exchange occurs and the faster the snow melts.

Section Summary

  • Most substances can exist either in solid, liquid, and gas forms, which are referred to as “phases.”
  • Phase changes occur at fixed temperatures for a given substance at a given pressure, and these temperatures are called boiling and freezing (or melting) points.
  • During phase changes, heat absorbed or released is given by: Q = mL where L is the latent heat coefficient.

Conceptual Questions

  1. Heat transfer can cause temperature and phase changes. What else can cause these changes?
  2. How does the latent heat of fusion of water help slow the decrease of air temperatures, perhaps preventing temperatures from falling significantly below ºC, in the vicinity of large bodies of water?
  3. What is the temperature of ice right after it is formed by freezing water?
  4. If you place ºC ice into ºC water in an insulated container, what will happen? Will some ice melt, will more water freeze, or will neither take place?
  5. What effect does condensation on a glass of ice water have on the rate at which the ice melts? Will the condensation speed up the melting process or slow it down?
  6. In very humid climates where there are numerous bodies of water, such as in Florida, it is unusual for temperatures to rise above about 35ºC (95ºF). In deserts, however, temperatures can rise far above this. Explain how the evaporation of water helps limit high temperatures in humid climates.
  7. In winters, it is often warmer in San Francisco than in nearby Sacramento, 150 km inland. In summers, it is nearly always hotter in Sacramento. Explain how the bodies of water surrounding San Francisco moderate its extreme temperatures.
  8. Putting a lid on a boiling pot greatly reduces the heat transfer necessary to keep it boiling. Explain why.
  9. Freeze-dried foods have been dehydrated in a vacuum. During the process, the food freezes and must be heated to facilitate dehydration. Explain both how the vacuum speeds up dehydration and why the food freezes as a result.
  10. When still air cools by radiating at night, it is unusual for temperatures to fall below the dew point. Explain why.
  11. In a physics classroom demonstration, an instructor inflates a balloon by mouth and then cools it in liquid nitrogen. When cold, the shrunken balloon has a small amount of light blue liquid in it, as well as some snow-like crystals. As it warms up, the liquid boils, and part of the crystals sublimate, with some crystals lingering for awhile and then producing a liquid. Identify the blue liquid and the two solids in the cold balloon. Justify your identifications using data from Table 1.

Problems & Exercises

  1. How much heat transfer (in kilocalories) is required to thaw a 0.450-kg package of frozen vegetables originally at 0ºC if their heat of fusion is the same as that of water?
  2. A bag containing 0ºC ice is much more effective in absorbing energy than one containing the same amount of 0ºC water. (a) How much heat transfer is necessary to raise the temperature of 0.800 kg of water from 0ºC to 30.0ºC? (b) How much heat transfer is required to first melt 0.800 kg of 0ºC ice and then raise its temperature? (c) Explain how your answer supports the contention that the ice is more effective.
  3. (a) How much heat transfer is required to raise the temperature of a 0.750-kg aluminum pot containing 2.50 kg of water from 30.0ºC to the boiling point and then boil away 0.750 kg of water? (b) How long does this take if the rate of heat transfer is 500 W 1 watt = 1 joule/second (1 W = 1 J/s)?
  4. The formation of condensation on a glass of ice water causes the ice to melt faster than it would otherwise. If 8.00 g of condensation forms on a glass containing both water and 200 g of ice, how many grams of the ice will melt as a result? Assume no other heat transfer occurs.
  5. On a trip, you notice that a 3.50-kg bag of ice lasts an average of one day in your cooler. What is the average power in watts entering the ice if it starts at 0ºC and completely melts to 0ºC water in exactly one day 1 watt = 1 joule/second (1 W = 1 J/s)?
  6. On a certain dry sunny day, a swimming pool’s temperature would rise by 1.50ºC if not for evaporation. What fraction of the water must evaporate to carry away precisely enough energy to keep the temperature constant?
  7. (a) How much heat transfer is necessary to raise the temperature of a 0.200-kg piece of ice from −20.0ºC to 130ºC, including the energy needed for phase changes? (b) How much time is required for each stage, assuming a constant 20.0 kJ/s rate of heat transfer? (c) Make a graph of temperature versus time for this process.
  8. In 1986, a gargantuan iceberg broke away from the Ross Ice Shelf in Antarctica. It was approximately a rectangle 160 km long, 40.0 km wide, and 250 m thick. (a) What is the mass of this iceberg, given that the density of ice is 917 kg/m3? (b) How much heat transfer (in joules) is needed to melt it? (c) How many years would it take sunlight alone to melt ice this thick, if the ice absorbs an average of 100 W/m2, 12.00 h per day?
  9. How many grams of coffee must evaporate from 350 g of coffee in a 100-g glass cup to cool the coffee from 95.0ºC to 45.0ºC? You may assume the coffee has the same thermal properties as water and that the average heat of vaporization is 2340 kJ/kg (560 cal/g). (You may neglect the change in mass of the coffee as it cools, which will give you an answer that is slightly larger than correct.)
  10. (a) It is difficult to extinguish a fire on a crude oil tanker, because each liter of crude oil releases 2.80 × 107 J of energy when burned. To illustrate this difficulty, calculate the number of liters of water that must be expended to absorb the energy released by burning 1.00 L of crude oil, if the water has its temperature raised from 20.0ºC to 100ºC, it boils, and the resulting steam is raised to 300ºC. (b) Discuss additional complications caused by the fact that crude oil has a smaller density than water.
  11. The energy released from condensation in thunderstorms can be very large. Calculate the energy released into the atmosphere for a small storm of radius 1 km, assuming that 1.0 cm of rain is precipitated uniformly over this area.
  12. To help prevent frost damage, 4.00 kg of 0ºC water is sprayed onto a fruit tree. (a) How much heat transfer occurs as the water freezes? (b) How much would the temperature of the 200-kg tree decrease if this amount of heat transferred from the tree? Take the specific heat to be 3.35 kJ/kg · ºC, and assume that no phase change occurs.
  13. A 0.250-kg aluminum bowl holding 0.800 kg of soup at 25.0ºC is placed in a freezer. What is the final temperature if 377 kJ of energy is transferred from the bowl and soup, assuming the soup’s thermal properties are the same as that of water?
  14. A 0.0500-kg ice cube at −30.0ºC is placed in 0.400 kg of 35.0ºC water in a very well-insulated container. What is the final temperature?
  15. If you pour 0.0100 kg of 20.0ºC water onto a 1.20-kg block of ice (which is initially at −15.0ºC), what is the final temperature? You may assume that the water cools so rapidly that effects of the surroundings are negligible.
  16. Indigenous people sometimes cook in watertight baskets by placing hot rocks into water to bring it to a boil. What mass of 500ºC rock must be placed in 4.00 kg of 15.0ºC water to bring its temperature to 100ºC, if 0.0250 kg of water escapes as vapor from the initial sizzle? You may neglect the effects of the surroundings and take the average specific heat of the rocks to be that of granite.
  17. What would be the final temperature of the pan and water in Calculating the Final Temperature When Heat Is Transferred Between Two Bodies: Pouring Cold Water in a Hot Pan if 0.260 kg of water was placed in the pan and 0.0100 kg of the water evaporated immediately, leaving the remainder to come to a common temperature with the pan?
  18. In some countries, liquid nitrogen is used on dairy trucks instead of mechanical refrigerators. A 3.00-hour delivery trip requires 200 L of liquid nitrogen, which has a density of 808 kg/m3. (a) Calculate the heat transfer necessary to evaporate this amount of liquid nitrogen and raise its temperature to 3.00ºC. (Use cp and assume it is constant over the temperature range.) This value is the amount of cooling the liquid nitrogen supplies. (b) What is this heat transfer rate in kilowatt-hours? (c) Compare the amount of cooling obtained from melting an identical mass of 0ºC ice with that from evaporating the liquid nitrogen.
  19. Some gun fanciers make their own bullets, which involves melting and casting the lead slugs. How much heat transfer is needed to raise the temperature and melt 0.500 kg of lead, starting from 25.0ºC?

Glossary

heat of sublimation: the energy required to change a substance from the solid phase to the vapor phase

latent heat coefficient: a physical constant equal to the amount of heat transferred for every 1 kg of a substance during the change in phase of the substance

sublimation: the transition from the solid phase to the vapor phase

Selected Solutions to Problems & Exercises

1. 35.9 kcal

3. (a) 591 kcal; (b) 4.94 × 103 s

5. 13.5 W

7. (a) 148 kcal; (b) 0.418 s, 3.34 s, 4.19 s, 22.6 s, 0.456 s

9. 33.0 g

10. (a) 9.67 L; (b) Crude oil is less dense than water, so it floats on top of the water, thereby exposing it to the oxygen in the air, which it uses to burn. Also, if the water is under the oil, it is less efficient in absorbing the heat generated by the oil.

12. (a) 319 kcal; (b) 2.00ºC

14. 20.6ºC

16. 4.38 kg

18. (a) 1.57 × 104 kcal; (b) 18.3 kW ⋅ h; (c) 1.29 × 104 kcal

  1. Values quoted at the normal melting and boiling temperatures at standard atmospheric pressure (1 atm). ↵
  2. At 37.0ºC (body temperature), the heat of vaporization Lv for water is 2430 kJ/kg or 580 kcal/kg ↵
  3. At 37.0ºC (body temperature), the heat of vaporization Lv for water is 2430 kJ/kg or 580 kcal/kg ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Physics Copyright © by Lumen Learning is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book