13 Unit Conversions and Dimensional Analysis
Learning Objectives
By the end of this section, you will be able to:
- Explain the dimensional analysis (factor label) approach to mathematical calculations involving quantities
- Use dimensional analysis to carry out unit conversions for a given property and computations involving two or more properties
It is often the case that a quantity of interest may not be easy (or even possible) to measure directly but instead must be calculated from other directly measured properties and appropriate mathematical relationships. For example, consider measuring the average speed of an athlete running sprints. This is typically accomplished by measuring the time required for the athlete to run from the starting line to the finish line, and the distance between these two lines, and then computing speed from the equation that relates these three properties:
[latex]\text{speed}=\frac{\text{distance}}{\text{time}}[/latex]
An Olympic-quality sprinter can run 100 m in approximately 10 s, corresponding to an average speed of [latex]\frac{\text{100 m}}{\text{10 s}}=\text{10 m/s}[/latex].
Note that this simple arithmetic involves dividing the numbers of each measured quantity to yield the number of the computed quantity (100/10 = 10) and likewise dividing the units of each measured quantity to yield the unit of the computed quantity (m/s = m/s). Now, consider using this same relation to predict the time required for a person running at this speed to travel a distance of 25 m. The same relation between the three properties is used, but in this case, the two quantities provided are a speed (10 m/s) and a distance (25 m). To yield the sought property, time, the equation must be rearranged appropriately:
[latex]\text{time}=\frac{\text{distance}}{\text{speed}}[/latex]
The time can then be computed as [latex]\frac{\text{25 m}}{\text{10 m/s}}=\text{2.5 s}[/latex].
Again, arithmetic on the numbers (25/10 = 2.5) was accompanied by the same arithmetic on the units (m/m/s = s) to yield the number and unit of the result, 2.5 s. Note that, just as for numbers, when a unit is divided by an identical unit (in this case, m/m), the result is “1”—or, as commonly phrased, the units “cancel.”
These calculations are examples of a versatile mathematical approach known as dimensional analysis (or the factor-label method). Dimensional analysis is based on this premise: the units of quantities must be subjected to the same mathematical operations as their associated numbers. This method can be applied to computations ranging from simple unit conversions to more complex, multi-step calculations involving several different quantities.
Conversion Factors and Dimensional Analysis
A ratio of two equivalent quantities expressed with different measurement units can be used as a unit conversion factor. For example, the lengths of 2.54 cm and 1 in. are equivalent (by definition), and so a unit conversion factor may be derived from the ratio,
[latex]\frac{\text{2.54 cm}}{\text{1 in.}}\text{(2.54 cm}=\text{1 in.) or 2.54}\frac{\text{cm}}{\text{in.}}[/latex]
Several other commonly used conversion factors are given in Table 1.
| Table 1. Common Conversion Factors | ||
|---|---|---|
| Length | Volume | Mass |
| 1 m = 1.0936 yd | 1 L = 1.0567 qt | 1 kg = 2.2046 lb |
| 1 in. = 2.54 cm (exact) | 1 qt = 0.94635 L | 1 lb = 453.59 g |
| 1 km = 0.62137 mi | 1 ft3 = 28.317 L | 1 (avoirdupois) oz = 28.349 g |
| 1 mi = 1609.3 m | 1 tbsp = 14.787 mL | 1 (troy) oz = 31.103 g |
When we multiply a quantity (such as distance given in inches) by an appropriate unit conversion factor, we convert the quantity to an equivalent value with different units (such as distance in centimeters). For example, a basketball player’s vertical jump of 34 inches can be converted to centimeters by:
[latex]\text{34 in.}\times \frac{\text{2.54 cm}}{1\cancel{\text{in.}}}=\text{86 cm}[/latex]
Since this simple arithmetic involves quantities, the premise of dimensional analysis requires that we multiply both numbers and units. The numbers of these two quantities are multiplied to yield the number of the product quantity, 86, whereas the units are multiplied to yield [latex]\frac{\text{in.}\times \text{cm}}{\text{in.}}[/latex] . Just as for numbers, a ratio of identical units is also numerically equal to one, [latex]\frac{\text{in.}}{\text{in.}}=\text{1,}[/latex] and the unit product thus simplifies to cm. (When identical units divide to yield a factor of 1, they are said to “cancel.”) Using dimensional analysis, we can determine that a unit conversion factor has been set up correctly by checking to confirm that the original unit will cancel, and the result will contain the sought (converted) unit.
Example 1: Using a Unit Conversion Factor
The mass of a competition frisbee is 125 g. Convert its mass to ounces using the unit conversion factor derived from the relationship 1 oz = 28.349 g (Table 1).
Show Answer
If we have the conversion factor, we can determine the mass in kilograms using an equation similar the one used for converting length from inches to centimeters.
[latex]x\text{ oz}=\text{125 g}\times \text{unit conversion factor}[/latex]
We write the unit conversion factor in its two forms:
[latex]\frac{\text{1 oz}}{\text{28.35 g}}\text{ and }\frac{\text{28.349 g}}{\text{1 oz}}[/latex]
The correct unit conversion factor is the ratio that cancels the units of grams and leaves ounces.
[latex]\begin{array}{ccc}x\text{ oz}\hfill & \text{=}\hfill & 125\cancel{\text{g}}\times \frac{\text{1 oz}}{\text{28.349}\cancel{\text{g}}}\hfill \\ \hfill & =\hfill & \left(\frac{125}{\text{28.349}}\right)\text{oz}\hfill \\ \hfill & =\hfill & \text{4.41 oz (three significant figures)}\hfill \end{array}[/latex]
Check Your Learning
Convert a volume of 9.345 qt to liters.
Show Answer
8.844 L
Beyond simple unit conversions, the factor-label method can be used to solve more complex problems involving computations. Regardless of the details, the basic approach is the same—all the factors involved in the calculation must be appropriately oriented to insure that their labels (units) will appropriately cancel and/or combine to yield the desired unit in the result. This is why it is referred to as the factor-label method. As your study of chemistry continues, you will encounter many opportunities to apply this approach.
Example 2: Computing Quantities from Measurement Results and Known Mathematical Relations
What is the density of common antifreeze in units of g/mL? A 4.00-qt sample of the antifreeze weighs 9.26 lb.
Show Answer
Since [latex]\text{density}=\frac{\text{mass}}{\text{volume}}[/latex] , we need to divide the mass in grams by the volume in milliliters. In general: the number of units of B = the number of units of A × unit conversion factor. The necessary conversion factors are given in Table 1.6: 1 lb = 453.59 g; 1 L = 1.0567 qt; 1 L = 1,000 mL. We can convert mass from pounds to grams in one step:
[latex]\text{9.26}\cancel{\text{lb}}\times \frac{\text{453.59 g}}{1\cancel{\text{lb}}}=4.20\times {10}^{3}\text{g}[/latex]
We need to use two steps to convert volume from quarts to milliliters.
- Convert quarts to liters: [latex]\text{4.00}\cancel{\text{qt}}\times \frac{\text{1 L}}{\text{1.0567}\cancel{\text{qt}}}=\text{3.78 L}[/latex]
- Convert liters to milliliters: [latex]\text{3.78}\cancel{\text{L}}\times \frac{\text{1000 mL}}{1\cancel{\text{L}}}=3.78\times {10}^{3}\text{mL}[/latex]
Then, [latex]\text{density}=\frac{\text{4.20}\times {10}^{3}\text{g}}{3.78\times {10}^{3}\text{mL}}=\text{1.11 g/mL}[/latex].
Alternatively, the calculation could be set up in a way that uses three unit conversion factors sequentially as follows:
[latex]\frac{\text{9.26}\cancel{\text{lb}}}{\text{4.00}\cancel{\text{qt}}}\times \frac{\text{453.59 g}}{1\cancel{\text{lb}}}\times \frac{\text{1.0567}\cancel{\text{qt}}}{1\cancel{\text{L}}}\times \frac{1\cancel{\text{L}}}{\text{1000 mL}}=\text{1.11 g/mL}[/latex]
Check Your Learning
What is the volume in liters of 1.000 oz, given that 1 L = 1.0567 qt and 1 qt = 32 oz (exactly)?
Show Answer
[latex]2.956\times {10}^{-2}\text{L}[/latex]
Example 3: Computing Quantities from Measurement Results and Known Mathematical Relations
While being driven from Philadelphia to Atlanta, a distance of about 1250 km, a 2014 Lamborghini Aventador Roadster uses 213 L gasoline.
- What (average) fuel economy, in miles per gallon, did the Roadster get during this trip?
- If gasoline costs $3.80 per gallon, what was the fuel cost for this trip?
Show Answer
Part 1
We first convert distance from kilometers to miles: [latex]\text{1250 km}\times \frac{\text{0.62137 mi}}{\text{1 km}}=\text{777 mi}[/latex]
Then we convert volume from liters to gallons: [latex]213\cancel{\text{L}}\times \frac{\text{1.0567}\cancel{\text{qt}}}{1\cancel{\text{L}}}\times \frac{\text{1 gal}}{4\cancel{\text{qt}}}=\text{56.3 gal}[/latex]
Then,
[latex]\text{(average) mileage}=\frac{\text{777 mi}}{\text{56.3 gal}}=\text{13.8 miles/gallon}=\text{13.8 mpg}[/latex]
Alternatively, the calculation could be set up in a way that uses all the conversion factors sequentially, as follows:
[latex]\frac{1250\cancel{\text{km}}}{213\cancel{\text{L}}}\times \frac{\text{0.62137 mi}}{1\cancel{\text{km}}}\times \frac{1\cancel{\text{L}}}{\text{1.0567}\cancel{\text{qt}}}\times \frac{4\cancel{\text{qt}}}{\text{1 gal}}=\text{13.8 mpg}[/latex]
Part 2
Using the previously calculated volume in gallons, we find: [latex]56.3\text{ gal}\times\frac{\$3.80}{1\text{ gal}}=\$214[/latex]
Check Your Learning
A Toyota Prius Hybrid uses 59.7 L gasoline to drive from San Francisco to Seattle, a distance of 1300 km (two significant digits).
- What (average) fuel economy, in miles per gallon, did the Prius get during this trip?
- If gasoline costs $3.90 per gallon, what was the fuel cost for this trip?
Show Answer
- 51 mpg
- $62
Exercises
Volume
- The label on a soft drink bottle gives the volume in two units: 2.0 L and 67.6 fl oz. Use this information to derive a conversion factor between the English and metric units. How many significant figures can you justify in your conversion factor?
- The label on a box of cereal gives the mass of cereal in two units: 978 grams and 34.5 oz. Use this information to find a conversion factor between the English and metric units. How many significant figures can you justify in your conversion factor?
- How many milliliters of a soft drink are contained in a 12.0-oz can?
- A barrel of oil is exactly 42 gal. How many liters of oil are in a barrel?
- Many medical laboratory tests are run using 5.0 μL blood serum. What is this volume in milliliters?
- Milk is sold by the liter in many countries. What is the volume of exactly 1/2 gal of milk in liters?
- Gasoline is sold by the liter in many countries. How many liters are required to fill a 12.0-gal gas tank?
- Calculate these volumes.
- What is the volume of 11.3 g graphite, density = 2.25 g/cm3?
- What is the volume of 39.657 g bromine, density = 2.928 g/cm3?
- Calculate these volumes.
- What is the volume of 25 g iodine, density = 4.93 g/cm3?
- What is the volume of 3.28 g gaseous hydrogen, density = 0.089 g/L?
Show Selected Answers
1. [latex]\begin{array}{c}\frac{\text{2.0 L}}{\text{67.6 fl oz}}=\frac{\text{0.030 L}}{\text{1 fl oz}}\end{array}[/latex]
3. 355 mL
5. 5.0 × 10−3 mL
7. 45.4 L
9. (a) 5.1 mL; (b) 37 L
Mass
- Is a 197-lb weight lifter light enough to compete in a class limited to those weighing 90 kg or less?
- A very good 197-lb weight lifter lifted 192 kg in a move called the clean and jerk. What was the mass of the weight lifted in pounds?
- If an aspirin tablet contains 325 mg aspirin, how many grams of aspirin does it contain?
- A long ton is defined as exactly 2240 lb. What is this mass in kilograms?
- The gas tank of a certain luxury automobile holds 22.3 gallons according to the owner’s manual. If the density of gasoline is 0.8206 g/mL, determine the mass in kilograms and pounds of the fuel in a full tank.
- Calculate these masses.
- What is the mass of 6.00 cm3 of mercury, density = 13.5939 g/cm3?
- What is the mass of 25.0 mL octane, density = 0.702 g/cm3?
- Calculate these masses.
- What is the mass of 4.00 cm3 of sodium, density = 0.97 g/cm?
- What is the mass of 125 mL gaseous chlorine, density = 3.16 g/L?
Show Selected Answers
1. yes; weight = 89.4 kg
4. 1.0160 × 103 kg
6. (a) 81.6 g; (b) 17.6 g
Length
- The diameter of a red blood cell is about 3 × 10−4 in. What is its diameter in centimeters?
- The distance between the centers of the two oxygen atoms in an oxygen molecule is 1.21 × 10−8 cm. What is this distance in inches?
- A chemist’s 50-Trillion Angstrom Run (see Exercise 22) would be an archeologist’s 10,900 cubit run. How long is one cubit in meters and in feet? (1 Å = 1 × 10−8 cm)
- Many chemistry conferences have held a 50-Trillion Angstrom Run (two significant figures). How long is this run in kilometers and in miles? (1 Å = 1 × 10−10 m)
Show Selected Answers
1. 8 × 10−4 cm
3. 0.46 m; 1.5 ft/cubit
Exercises
- Write conversion factors (as ratios) for the number of:
- yards in 1 meter
- liters in 1 liquid quart
- pounds in 1 kilogram
- Write conversion factors (as ratios) for the number of:
- kilometers in 1 mile
- liters in 1 cubic foot
- grams in 1 ounce
- Soccer is played with a round ball having a circumference between 27 and 28 in. and a weight between 14 and 16 oz. What are these specifications in units of centimeters and grams?
- A woman’s basketball has a circumference between 28.5 and 29.0 inches and a maximum weight of 20 ounces (two significant figures). What are these specifications in units of centimeters and grams?
- Use scientific (exponential) notation to express the following quantities in terms of the SI base units in Table 1:
- 0.13 g
- 232 Gg
- 5.23 pm
- 86.3 mg
- 37.6 cm
- 54 μm
- 1 Ts
- 27 ps
- 0.15 mK
- Complete the following conversions between SI units.
- 612 g = ________ mg
- 8.160 m = ________ cm
- 3779 μg = ________ g
- 781 mL = ________ L
- 4.18 kg = ________ g
- 27.8 m = ________ km
- 0.13 mL = ________ L
- 1738 km = ________ m
- 1.9 Gg = ________ g
- Make the conversion indicated in each of the following:
- the men’s world record long jump, 29 ft 4¼ in., to meters
- the greatest depth of the ocean, about 6.5 mi, to kilometers
- the area of the state of Oregon, 96,981 mi2, to square kilometers
- the volume of 1 gill (exactly 4 oz) to milliliters
- the estimated volume of the oceans, 330,000,000 mi3, to cubic kilometers.
- the mass of a 3525-lb car to kilograms
- the mass of a 2.3-oz egg to grams
- Make the conversion indicated in each of the following:
- the length of a soccer field, 120 m (three significant figures), to feet
- the height of Mt. Kilimanjaro, at 19,565 ft the highest mountain in Africa, to kilometers
- the area of an 8.5 t 11-inch sheet of paper in cm2
- the displacement volume of an automobile engine, 161 in.3, to liters
- the estimated mass of the atmosphere, 5.6 t 1015 tons, to kilograms
- the mass of a bushel of rye, 32.0 lb, to kilograms
- the mass of a 5.00-grain aspirin tablet to milligrams (1 grain = 0.00229 oz)
- As an instructor is preparing for an experiment, he requires 225 g phosphoric acid. The only container readily available is a 150-mL Erlenmeyer flask. Is it large enough to contain the acid, whose density is 1.83 g/mL?
- To prepare for a laboratory period, a student lab assistant needs 125 g of a compound. A bottle containing 1/4 lb is available. Did the student have enough of the compound?
- 27 A chemistry student is 159 cm tall and weighs 45.8 kg. What is her height in inches and weight in pounds?
- In a recent Grand Prix, the winner completed the race with an average speed of 229.8 km/h. What was his speed in miles per hour, meters per second, and feet per second?
- Solve these problems about lumber dimensions.
- To describe to a European how houses are constructed in the US, the dimensions of “two-by-four” lumber must be converted into metric units. The thickness × width × length dimensions are 1.50 in. × 3.50 in. × 8.00 ft in the US. What are the dimensions in cm × cm × m?
- This lumber can be used as vertical studs, which are typically placed 16.0 in. apart. What is that distance in centimeters?
- Calculate the density of aluminum if 27.6 cm3 has a mass of 74.6 g.
- Osmium is one of the densest elements known. What is its density if 2.72 g has a volume of 0.121 cm3?
Show Selected Answers
1. (a) [latex]\frac{\text{1.0936 yd}}{\text{1 m}}[/latex] ; (b) [latex]\frac{\text{0.94635 L}}{\text{1 qt}}[/latex] ; (c) [latex]\frac{\text{2.2046 lb}}{\text{1 kg}}[/latex]
3. 68–71 cm; 400–450 g
5. (a) 1.3 × 10−4 kg; (b) 2.32 × 108 kg; (c) 5.23 × 10−12 m; (d) 8.63 × 10−5 kg; (e) 3.76 × 10−1 m; (f) 5.4 × 10−5 m; (g) 1 × 1012 s; (h) 2.7 × 10−11 s; (i) 1.5 × 10−4 K
8. (a) 394 ft (b) 5.9634 km (c) 6.0 × 102 (d) 2.64 L (e) 5.1 × 1018 kg (f) 14.5 kg (g) 324 mg
9. Yes, the acid’s volume is 123 mL.
11. 62.6 in (about 5 ft 3 in.) and 101 lb
13. (a) 3.81 cm × 8.89 cm × 2.44 m; (b) 40.6 cm
14. 2.70 g/cm3
Conversion of Temperature Units
We use the word temperature to refer to the hotness or coldness of a substance. One way we measure a change in temperature is to use the fact that most substances expand when their temperature increases and contract when their temperature decreases. The mercury or alcohol in a common glass thermometer changes its volume as the temperature changes. Because the volume of the liquid changes more than the volume of the glass, we can see the liquid expand when it gets warmer and contract when it gets cooler.
To mark a scale on a thermometer, we need a set of reference values: Two of the most commonly used are the freezing and boiling temperatures of water at a specified atmospheric pressure. On the Celsius scale, 0 °C is defined as the freezing temperature of water and 100 °C as the boiling temperature of water. The space between the two temperatures is divided into 100 equal intervals, which we call degrees. On the Fahrenheit scale, the freezing point of water is defined as 32 °F and the boiling temperature as 212 °F. The space between these two points on a Fahrenheit thermometer is divided into 180 equal parts (degrees).
Defining the Celsius and Fahrenheit temperature scales as described in the previous paragraph results in a slightly more complex relationship between temperature values on these two scales than for different units of measure for other properties. Most measurement units for a given property are directly proportional to one another (y = mx). Using familiar length units as one example:
[latex]\text{length in feet}=\left(\frac{\text{1 ft}}{\text{12 in.}}\right)\times \text{length in inches}[/latex]
where y = length in feet, x = length in inches, and the proportionality constant, m, is the conversion factor. The Celsius and Fahrenheit temperature scales, however, do not share a common zero point, and so the relationship between these two scales is a linear one rather than a proportional one (y = mx + b). Consequently, converting a temperature from one of these scales into the other requires more than simple multiplication by a conversion factor, m, it also must take into account differences in the scales’ zero points (b).
The linear equation relating Celsius and Fahrenheit temperatures is easily derived from the two temperatures used to define each scale. Representing the Celsius temperature as x and the Fahrenheit temperature as y, the slope, m, is computed to be:
[latex]\displaystyle{m}=\frac{\Delta y}{\Delta x}=\frac{212^{\circ}\text{ F}-32^{\circ}\text{ F}}{100^{\circ}\text{ C}-0^{\circ}\text{ C}}=\frac{180^{\circ}\text{ F}}{100^{\circ}\text{ C}}=\frac{9^{\circ}\text{ F}}{5^{\circ}\text{ C}}[/latex]
The y-intercept of the equation, b, is then calculated using either of the equivalent temperature pairs, (100 °C, 212 °F) or (0 °C, 32 °F), as:
[latex]b=y-mx=32^{\circ}\text{ F}-\frac{9 ^{\circ}\text{ F}}{5 ^{\circ}\text{ C}}\times{0}^{\circ}\text{ C}=32^{\circ}\text{ F}[/latex]
The equation relating the temperature scales is then:
[latex]{T}_{\text{ }^{\circ}\text{F}}=\left(\frac{9^{\circ}\text{ F}}{5^{\circ}\text{ C}}\times{T}_{\text{ }^{\circ}\text{C}}\right)+32 ^{\circ}\text{ C}[/latex]
An abbreviated form of this equation that omits the measurement units is:
[latex]{T}_{\text{ }^{\circ}\text{F}}=\frac{9}{5}\times{T}_{^{\circ}\text{ C}}+32[/latex]
Rearrangement of this equation yields the form useful for converting from Fahrenheit to Celsius:
[latex]{T}_{\text{ }^{\circ}\text{C}}=\frac{5}{9}\left({T}_{^{\circ}\text{ F}}-32\right)[/latex]
As mentioned earlier in this chapter, the SI unit of temperature is the kelvin (K). Unlike the Celsius and Fahrenheit scales, the kelvin scale is an absolute temperature scale in which 0 (zero) K corresponds to the lowest temperature that can theoretically be achieved. The early 19th-century discovery of the relationship between a gas’s volume and temperature suggested that the volume of a gas would be zero at −273.15 °C. In 1848, British physicist William Thompson, who later adopted the title of Lord Kelvin, proposed an absolute temperature scale based on this concept (further treatment of this topic is provided in this text’s chapter on gases).
The freezing temperature of water on this scale is 273.15 K and its boiling temperature 373.15 K. Notice the numerical difference in these two reference temperatures is 100, the same as for the Celsius scale, and so the linear relation between these two temperature scales will exhibit a slope of [latex]1\frac{\text{K}}{^{\circ}\text{C}}[/latex] . Following the same approach, the equations for converting between the kelvin and Celsius temperature scales are derived to be:
[latex]{T}_{\text{K}}={T}_{^{\circ}\text{C}}+\text{273.15}[/latex]
[latex]{T}_{\text{ }^{\circ}\text{C}}={T}_{\text{K}}-\text{273.15}[/latex]
The 273.15 in these equations has been determined experimentally, so it is not exact. Figure 1 shows the relationship among the three temperature scales. Recall that we do not use the degree sign with temperatures on the kelvin scale.
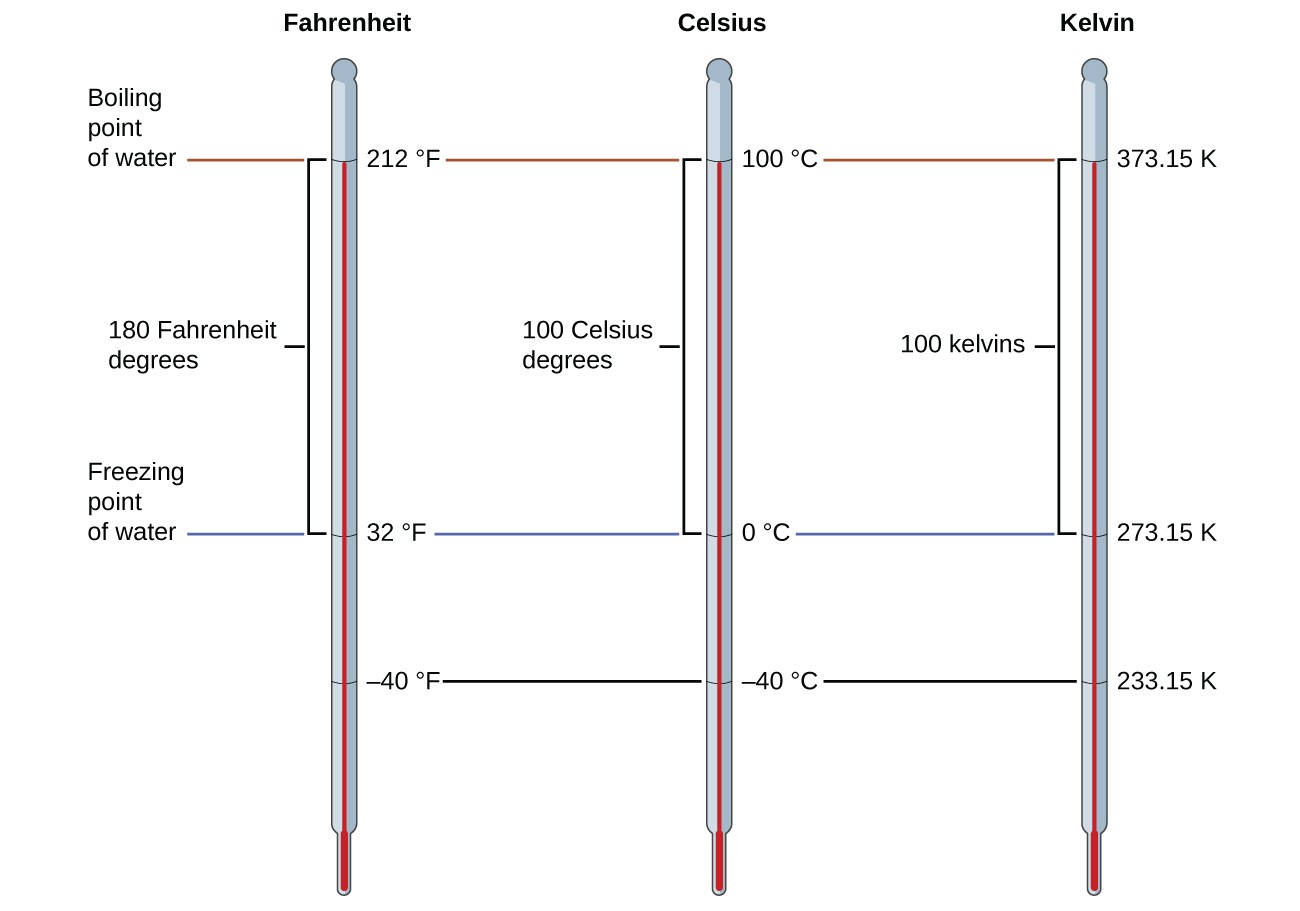
Although the kelvin (absolute) temperature scale is the official SI temperature scale, Celsius is commonly used in many scientific contexts and is the scale of choice for nonscience contexts in almost all areas of the world. Very few countries (the U.S. and its territories, the Bahamas, Belize, Cayman Islands, and Palau) still use Fahrenheit for weather, medicine, and cooking.
Example 4: Conversion from Celsius
Normal body temperature has been commonly accepted as 37.0 °C (although it varies depending on time of day and method of measurement, as well as among individuals). What is this temperature on the kelvin scale and on the Fahrenheit scale?
Show Answer
[latex]\text{K}=\text{ }^{\circ}\text{C}+273.15=37.0+273.2=\text{310.2 K}[/latex]
[latex]\text{ }^{\circ}\text{F}=\frac{9}{5}^{\circ}\text{ C}+32.0=\left(\frac{9}{5}\times 37.0\right)+32.0=66.6+32.0=98.6^{\circ}\text{ F}[/latex]
Check Your Learning
Convert 80.92 °C to K and °F.
Show Answer
354.07 K, 177.7 °F
Example 5: Conversion from Fahrenheit
Baking a ready-made pizza calls for an oven temperature of 450 °F. If you are in Europe, and your oven thermometer uses the Celsius scale, what is the setting? What is the kelvin temperature?
Show Answer
[latex]\text{ }^{\circ}\text{C}=\frac{5}{9}(^{\circ}\text{ F}-\text{32)}=\frac{5}{9}\left(450-32\right)=\frac{5}{9}\times 418=232^{\circ}\text{ C}\rightarrow\text{set oven to 230}^{\circ}\text{ C}\left(\text{two significant figures}\right)[/latex]
[latex]\text{K}=\text{ }^{\circ}\text{ C}+273.15=230+273=\text{503 K}\rightarrow 5.0\times {10}^{2}\text{K}\left(\text{two significant figures}\right)[/latex]
Check Your Learning
Convert 50 °F to °C and K.
Show Answer
10 °C, 280 K
Key Concepts and Summary
Measurements are made using a variety of units. It is often useful or necessary to convert a measured quantity from one unit into another. These conversions are accomplished using unit conversion factors, which are derived by simple applications of a mathematical approach called the factor-label method or dimensional analysis. This strategy is also employed to calculate sought quantities using measured quantities and appropriate mathematical relations.
Key Equations
- [latex]{T}_{^{\circ}\text{C}}=\frac{5}{9}\times {T}_{^{\circ}\text{F}}-32[/latex]
- [latex]{T}_{^{\circ}\text{F}}=\frac{9}{5}\times {T}_{^{\circ}\text{C}}+32[/latex]
- [latex]{T}_{\text{K}}=\text{ }^{\circ}\text{C}+273.15[/latex]
- [latex]{T}_{^{\circ}\text{C}}=\text{K}-273.15[/latex]
Exercises
- Convert the boiling temperature of gold, 2966 °C, into degrees Fahrenheit and kelvin.
- Convert the temperature of scalding water, 54 °C, into degrees Fahrenheit and kelvin.
- Convert the temperature of the coldest area in a freezer, −10 °F, to degrees Celsius and kelvin.
- Convert the temperature of dry ice, −77 °C, into degrees Fahrenheit and kelvin.
- Convert the boiling temperature of liquid ammonia, −28.1 °F, into degrees Celsius and kelvin.
- The label on a pressurized can of spray disinfectant warns against heating the can above 130 °F. What are the corresponding temperatures on the Celsius and kelvin temperature scales?
- The weather in Europe was unusually warm during the summer of 1995. The TV news reported temperatures as high as 45 °C. What was the temperature on the Fahrenheit scale?
Show Selected Answers
1. 5371 °F, 3239 K
3. −23 °C, 250 K
5. −33.4 °C, 239.8 K
7. 113 °F
Glossary
dimensional analysis: (also, factor-label method) versatile mathematical approach that can be applied to computations ranging from simple unit conversions to more complex, multi-step calculations involving several different quantities
Fahrenheit: unit of temperature; water freezes at 32 °F and boils at 212 °F on this scale
unit conversion factor: ratio of equivalent quantities expressed with different units; used to convert from one unit to a different unit

