45 9.5 Additional Information and Full Hypothesis Test Examples
- In a hypothesis test problem, you may see words such as “the level of significance is 1%.” The “1%” is the preconceived or preset α.
- The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data.
- If no level of significance is given, a common standard to use is α = 0.05.
- When you calculate the p-value and draw the picture, the p-value is the area in the left tail, the right tail, or split evenly between the two tails. For this reason, we call the hypothesis test left, right, or two tailed.
- The alternative hypothesis, Ha, tells you if the test is left, right, or two-tailed. It is the key to conducting the appropriate test.
- Ha never has a symbol that contains an equal sign.
- Thinking about the meaning of the p-value: A data analyst (and anyone else) should have more confidence that he made the correct decision to reject the null hypothesis with a smaller p-value (for example, 0.001 as opposed to 0.04) even if using the 0.05 level for alpha. Similarly, for a large p-value such as 0.4, as opposed to a p-value of 0.056 (alpha = 0.05 is less than either number), a data analyst should have more confidence that she made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.
The following examples illustrate a left-, right-, and two-tailed test.
Example 1
Ho: μ = 5
Ha: μ < 5
Significance level = 5%
Assume the p-value is 0.0243.
- What type of test is this?
- Determine if the test is left, right, or two-tailed.
- Draw the picture of the p-value.
- Do we reject null hypothesis, H0: μ = 5?
- Do we have enough evidence to conclude that μ < 5?
Click here to show solution:
- Test of a single population mean.
- Ha tells you the test is left-tailed.
- The picture of the p-value is as follows:

- Since p-value < significance level, we reject null hypothesis, Ho: μ = 5.
- We have enough evidence to conclude that Ha: μ < 5.
Try It
H0: μ = 10
Ha: μ < 10
Significance level = 5% = 0.05
Assume the p-value is 0.0435.
- What type of test is this?
- Determine if the test is left, right, or two-tailed.
- Draw the picture of the p-value.
- Do we reject null hypothesis, H0: μ = 10?
- Do we have enough evidence to conclude that μ < 10?
[practice-area rows=”1″][/practice-area]
Click here to show solution:
- Test of a single population mean.
- left-tailed test
- The picture of the p-value is as follows:

- Since p-value < significance level, we reject null hypothesis, H0: μ = 10.
- We have enough evidence to conclude Ha: μ < 10.
Example 2
Ha: p > 0.2
Significance level = 0.05
Assume the p-value is 0.0719.
- What type of test is this?
- Determine if the test is left, right, or two-tailed.
- Draw the picture of the p-value.
- Do we reject null hypothesis, H0: p ≤ 0.2?
- Do we have enough evidence to conclude that p > 0.2?
Click here to show solution:
- This is a test of a single population proportion.
- Ha tells you the test is right-tailed.
- The picture of the p-value is as follows:

- Since p-value > significance level, we do not reject null hypothesis (H0: p ≤ 0.2).
- We do not have enough evidence to conclude Ha: p > 0.2.
Try It
H0: μ ≤ 1
Ha: μ > 1
Significance level = 1%
Assume the p-value is 0.1243.
- What type of test is this?
- Determine if the test is left, right, or two-tailed.
- Draw the picture of the p-value.
- Do we reject null hypothesis, H0: μ ≤ 1?
- Do we have enough evidence to conclude that μ > 1?
Show Answer
- Test of a population mean.
- right-tailed test
- The picture of the p-value is as follows:

- Since p-value > significance level, we do not reject null hypothesis, H0: μ ≤ 1.
- We do not have enough evidence to conclude that μ > 1.
Example 3
Ha: p ≠ 50
Significance level = 1%
Assume the p-value is 0.0005
- What type of test is this?
- Determine if the test is left, right, or two-tailed.
- Draw the picture of the p-value.
- Do we reject null hypothesis, H0: p = 50?
- Do we have enough evidence to conclude that p ≠ 50?
Show Answer
- This is a test of a single population mean.
- Ha tells you the test is two-tailed.
- The picture of the p-value is as follows:
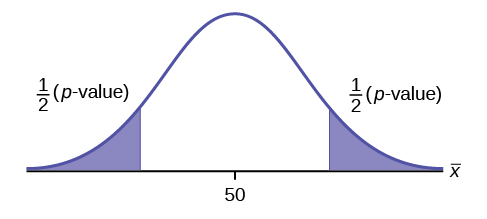
- Since p-value < significance level, we reject null hypothesis, H0: p = 50.
- We have enough evidence to conclude Ha: p ≠ 50.
Try It
H0: p = 0.5
Ha: p ≠ 0.5
Significance level = 0.05
Assume the p-value is 0.2564.
- What type of test is this?
- Determine if the test is left, right, or two-tailed.
- Draw the picture of the p-value.
- Do we reject null hypothesis, H0: p = 0.5?
- Do we have enough evidence to conclude that p ≠ 0.5?
Click here to show solution:
- Hypothesis test of a single population proportion.
- two-tailed test
- The picture of the p-value is as follows:

- Since p-value > significance level, we do not reject null hypothesis ( H0: p = 0.5).
- We do not have enough evidence to conclude Ha: p ≠ 0.5.
Steps to set up a hypothesis test:
|
Full Hypothesis Test Examples
Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds. His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims.
For the 15 swims, Jeffrey’s mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds.
Conduct a hypothesis test using 5% significance level. Assume that the swim times for the 25-yard freestyle are normal.
Solution:
mean = 16.43 seconds, standard deviation = 0.8 seconds.
Since the problem is about a mean, this is a test of a single population mean.
1. What are we testing?
H0: μ = 16.43
Ha: μ < 16.43
For Jeffrey to swim faster, his time will be less than 16.43 seconds. The “<” tells you this is left-tailed.
significance level, [latex]\alpha[/latex] = 5% = 0.052. What is the significance level?
3. What is the p-value?
Graph:
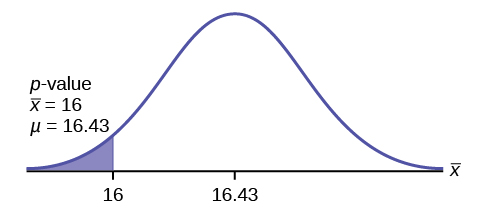
[latex]\overline{X}[/latex] = the mean time to swim the 25-yard freestyle.
[latex]\overline{X}[/latex] is normal. Population standard deviation is known: σ = 0.8
[latex]\overline{X}[/latex] = 16,
[latex]\mu[/latex] = 16.43 (comes from H0 and not the data.)
σ = 0.8, and
n = 15.
Calculate the p-value using the normal distribution for a mean:
p-value
= P[latex]\left(\overline{X}<{16}\right)[/latex]
= P[latex]\left(\frac{\overline{X} - {\mu}}{\frac{\sigma}{\sqrt{n}}}<\frac{16 - {\mu}}{\frac{\sigma}{\sqrt{n}}}\right)[/latex]
= P[latex]\left( Z <\frac{16 - {\mu}}{\frac{\sigma}{\sqrt{n}}}\right)[/latex]
= P[latex]\left( Z <\frac{16 -16.43}{\frac{0.8}{\sqrt{15}}}\right)[/latex]
= 0.0187
where the sample mean in the problem is given as 16.
4. Comparison between p-value and significance level.
p-value = 0.0187 (This is called the actual level of significance.)
The p-value is the area to the left of the sample mean is given as 16.
p-value = 0.0187, α = 0.05
Therefore, α > p-value.
|
Interpretation of the p-value: If H0 is true, there is a 0.0187 probability (1.87%)that Jeffrey’s mean time to swim the 25-yard freestyle is 16 seconds or less. Because a 1.87% chance is small, the mean time of 16 seconds or less is unlikely to have happened randomly. It is a rare event. |
5. Decision?
This means that you reject μ = 16.43. In other words, you do not think Jeffrey swims the 25-yard freestyle in 16.43 seconds but faster with the new goggles.
Make a decision: Since α > p-value, reject H0.
6. Conclusion?
At the 5% significance level, we conclude that Jeffrey swims faster using the new goggles. The sample data show there is sufficient evidence that Jeffrey’s mean time to swim the 25-yard freestyle is less than 16.43 seconds.
Using TI-Calculator to find p-value:
The calculator not only calculates the p-value (p = 0.0187), but it also calculates the test statistic (z-score) for the sample mean. Do this set of instructions again except arrow to Draw (instead of Calculate ) and press ENTER . A shaded graph appears with z = -2.08 (test statistic) and p = 0.0187 (p-value). Make sure when you use Draw that no other equations are highlighted in Y = and the plots are turned off. |
To find P[latex]\left(\overline{x}<{16}\right)[/latex], we will use TI-Calculator. Ti-Calculator: 2nd DISTR normcdf ([latex]{-10}^{99}[/latex], 16,16.43,[latex]\frac{{0.8}}{{\sqrt{15}}}[/latex]).
The Type I and Type II errors for this problem are as follows:
The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.)
The Type II error is that there is not evidence to conclude that Jeffrey swims the 25-yard free-style, on average, in less than 16.43 seconds when, in fact, he actually does swim the 25-yard free-style, on average, in less than 16.43 seconds. (Do not reject the null hypothesis when the null hypothesis is false.)
Try It
The mean throwing distance of a football for a Marco, a high school freshman quarterback, is 40 yards, with a standard deviation of 2 yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset α = 0.05. Assume the throw distances for footballs are normal.
First, determine what type of test this is, set up the hypothesis test, find the p-value, sketch the graph, and state your conclusion.
[practice-area rows=”4″][/practice-area]
Step-by-Step Solution
Since the problem is about a mean, this is a test of a single population mean.
- H0 : μ = 40
- Ha : μ > 40
- α = 0.05
- Z = [latex]\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}[/latex] = [latex]\frac{45 - 40}{\frac{2}{\sqrt{20}}}[/latex] = 11.1803
- When [latex]\overline{X}[/latex] = 45, its corresponding z-score is 11.1803.
The area to the right when [latex]\overline{X}[/latex] = 45
= The area to the right of z-score = 11.1803
= blue shaded area
= p-value
= [latex]2.6115*10^{-29}[/latex]

- Because p < α, we reject the null hypothesis.
- There is sufficient evidence to suggest that the change in grip improved Marco’s throwing distance.
Using TI-Calculator to solve:
- Press STAT and arrow over to TESTS.
- Press 1:Z-Test.
- Arrow over to Stats and press ENTER.
- Arrow down and enter 40 for μ0 (null hypothesis), 2 for σ, 45 for the sample mean, and 20 for n.
- Arrow down to μ: (alternative hypothesis) and set it either as <, ≠, or >.
- Press ENTER.
- Arrow down to Calculate and press ENTER.
The p-value = 0.0062. α = 0.05.
Because p < α, we reject the null hypothesis.
There is sufficient evidence to suggest that the change in grip improved Marco’s throwing distance.
The calculator not only calculates the p-value but it also calculates the test statistic (z-score) for the sample mean. Select <, ≠, or >; for the alternative hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate). Press ENTER. A shaded graph appears with test statistic and p-value. Make sure when you use Draw that no other equations are highlighted in Y = and the plots are turned off.
Example 4
A college football coach thought that his players could bench press a mean weight of 275 pounds. It is known that the standard deviation is 55 pounds. Three of his players thought that the mean weight was more than that amount. They asked 30 of their teammates for their estimated maximum lift on the bench press exercise. The data ranged from 205 pounds to 385 pounds. The actual different weights were (frequencies are in parentheses) 205(3) 215(3)225(1) 241(2) 252(2) 265(2) 275(2) 313(2) 316(5) 338(2) 341(1) 345(2) 368(2) 385(1).
Conduct a hypothesis test using a 2.5% level of significance to determine if the bench press mean is more than 275 pounds.
Solution:
1. What are we testing?
Since the problem is about a mean weight, this is a test of a single population mean.
H0: μ = 275
Ha: μ > 275
Significance leel, [latex]\alpha[/latex] = 2.5% = 0.025
This is a right-tailed test.
2. What is the significance level, [latex]\alpha[/latex]?
[latex]\alpha[/latex] = 2.5% = 0.025
3. Find the p-value.
[latex]\overline{X}[/latex] = the mean weight (in pounds) lifted by the football players.
Distribution for the test: X is normally distributed because σ is known.
[latex]\overline{x}[/latex] = 286.2, n = 30, σ = 55 pounds (Always use σ if you know it.)
We assume μ = 275 pounds unless our data shows us otherwise.
Calculate the p-value using the normal distribution for a mean and using the sample mean as input.
p-value
= P ([latex]\overline{x}[/latex] > 286.2 )
= P ([latex]\frac{\overline{x} - {\mu}}{\frac{\sigma}{\sqrt{n}}}[/latex] > [latex]\frac{286.2 - {\mu}}{\frac{\sigma}{\sqrt{n}}}[/latex] )
= P (Z > [latex]\frac{286.2 - {\mu}}{\frac{\sigma}{\sqrt{n}}}[/latex])
= P (Z > [latex]\frac{286.2 - 275}{\frac{55}{\sqrt{30}}}[/latex])
= P (Z > 1.1153623)
= 0.1323.
4. Comparison between p-value and significance level.
Interpretation of the p-value:
If H0 is true, then there is a 0.1331 probability (13.23%) that the football players can lift a mean weight of 286.2 pounds or more. Because a 13.23% chance is large enough, a mean weight lift of 286.2 pounds or more is not a rare event.
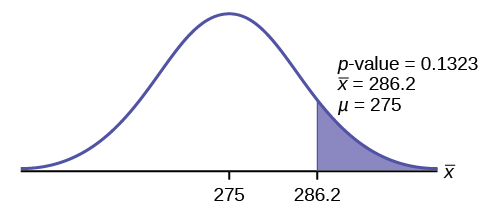
α = 0.025, p-value = 0.1323
5. Decision?
Make a decision: Since α <p-value, do not reject H0.
6. Conclusion?
Conclusion:
At the 2.5% level of significance, from the sample data, there is not sufficient evidence to conclude that the true mean weight lifted is more than 275 pounds.
The p-value can easily be calculated.
|
The calculator not only calculates the p-value (p = 0.1331, a little different from the previous calculation – in it we used the sample mean rounded to one decimal place instead of the data) but it also calculates the test statistic (z-score) for the sample mean, the sample mean, and the sample standard deviation. μ > 275 is the alternative hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with z = 1.112 (test statistic) and p = 0.1331 (p-value). Make sure when you use Draw that no other equations are highlighted in Y = and the plots are turned off.
Example 5
Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the scores 65 65 70 67 66 63 63 68 72 71. The data are assumed to be from a normal distribution.
He performs a hypothesis test using a 5% level of significance.
Solution:
1. What are we testing?
Since we do not know population standard deviation, we are going to run Student’s t Test.
This is a test of a single population mean.
H0: μ = 65
Ha: μ > 65
A 5% level of significance means that α = 0.05.
Since the instructor thinks the average score is higher, use a “>”. The “>” means the test is right-tailed.
2. What is the significance level, [latex]\alpha[/latex]?
The significance level, [latex]\alpha[/latex] = 5% = 0.05
3. Find the p-value.
Random variable: [latex]\overline{X}[/latex] = average score on the first statistics test.
Distribution for the test: If you read the problem carefully, you will notice that there is no population standard deviation given. You are only given n = 10 sample data values. Notice also that the data come from a normal distribution.
This means that the distribution for the test is a student’s t-test.
Use tdf. Therefore, the distribution for the test is t9 where n = 10 and df = 10 – 1 = 9.
Calculate the p-value using the Student’s t-distribution:
Given that sample mean and sample standard deviation are calculated as 67 and 3.1972 from the data,
p-value
= P([latex]\overline{x}[/latex]> 67)
= P([latex]\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}[/latex]> [latex]\frac{67 - 65}{\frac{3.1972}{\sqrt{10}}}[/latex])
= P( t > 1.978)
= 0.0396
4. Comparison between p-value and significance level.
Interpretation of the p-value:
If the null hypothesis is true, then there is a 0.0396 probability (3.96%) that the sample mean is 65 or more.
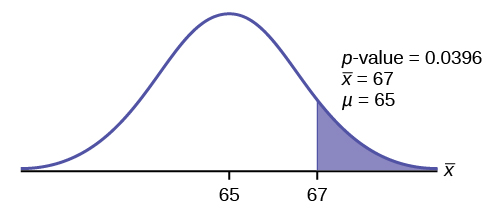
Since α = 0.05 and p-value = 0.0396. α > p-value.
5. Decision?
Since α > p-value, reject H0.
This means you reject μ = 65. In other words, you believe the average test score is more than 65.
6. Conclusion?
At a 5% level of significance, the sample data show sufficient evidence that the mean (average) test score is more than 65, just as the math instructor thinks.
The p-value can easily be calculated.
|
Try It
It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows:
$4, $3, $2, $3, $1, $7, $2, $1, $1, $2.
Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, find the p-value, state your conclusion, and identify the Type I and Type II errors.
Show Answer
We run Student’s t-test as we do not know the population standard deviation.
H0: μ = 5
Ha: μ < 5
p = 0.0082
Because p < α, we reject the null hypothesis. There is sufficient evidence to suggest that the stock price of the company grows at a rate less than $5 a week.
Type I Error: To conclude that the stock price is growing slower than $5 a week when, in fact, the stock price is growing at $5 a week (reject the null hypothesis when the null hypothesis is true).
Type II Error: To conclude that the stock price is growing at a rate of $5 a week when, in fact, the stock price is growing slower than $5 a week (do not reject the null hypothesis when the null hypothesis is false).
Example 6
Solution:
1. What are we testing?
This is a Normal test of a single population proportion.
H0: p = 0.50
Ha: p ≠ 0.50
The 1% level of significance means that α = 0.01.
The words “is different from” tell you this is a two-tailed test.
2. What is the significance level, [latex]\alpha[/latex]?
the significance level, [latex]\alpha[/latex] = 1% = 0.01
3. Find the p-value.
This is a two-tailed test. We will include both left tail and right tail in the hypothesis test.
P′ = the percent of of first-time brides who are younger than their grooms.
The proportion of first-time brides who reply that they are younger than their grooms in sample of 100 brides = [latex]\frac{53}{100}[/latex] = 0.53.
0.53 is the right tail of this test as 0.53 is larger than 0.5 (the population mean).
How about the left tail?
Since 0.53 is on the right side of 0.50, the left tail will fall on the left side of 0.50.
Moreover, 0.03 is the difference between 0.53 and 0.50. Hence the distance between the left tail and 0.50 is equal to 0.03 as well.
0.50 – 0.03 = 0.47.
The left tail of this test is 0.47.
Given that p = 0.50, q = 1 − p = 0.50, and n = 100,
p-value
= area to the right of right tail + area to the left of left tail
= area to the right of 0.53 + area to the left of 0.47
= P (p’ > 0.53) + P (p’ < 0.47)
= P ( [latex]\frac{p' - p}{\sqrt{\frac{pq}{n}}}[/latex] > [latex]\frac{0.53-0.50}{\sqrt{\frac{(0.5)(0.5)}{100}}}[/latex] ) + P ( [latex]\frac{p' - p}{\sqrt{\frac{pq}{n}}}[/latex] > [latex]\frac{0.47-0.50}{\sqrt{\frac{(0.5)(0.5)}{100}}}[/latex] )
= P ( Z > 0.6 ) + P(Z < -0.6 )
= 0.27425 + 0.27425
= 0.5485

4. Comparison between p-value and significance level.
p-value = 0.5485, significance level = 0.01
5. Decision?
Since p-value > significance level, we do not reject H0.
6. Conclusion?
There is no sufficient evidence to suggest that the percentage is different than 50%.
Solution (Using TI-Calculator)
- Press
STATand arrow over toTESTS. - Press
5:1-PropZTest. Enter .5 for p0, 53 for x and 100 for n. - Arrow down to
Propand arrow tonot equalsp0. PressENTER. - Arrow down to
Calculateand pressENTER. - The calculator calculates the p-value (p = 0.5485) and the test statistic (z-score).
Prop not equals.5 is the alternate hypothesis.
Do this set of instructions again except arrow to Draw (instead of Calculate). Press ENTER. A shaded graph appears with z = 0.6 (test statistic) and p = 0.5485 (p-value). Make sure when you use Draw that no other equations are highlighted in Y = and the plots are turned off.
Try It
A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.
First, determine what type of test this is, set up the hypothesis test, find the p-value, sketch the graph, and state your conclusion.
Show Answer
Since the problem is about percentages, this is a test of single population proportions.
H0 : p = 0.85
Ha: p ≠ 0.85
p = 0.7554
Because p > α, we fail to reject the null hypothesis.
There is not sufficient evidence to suggest that the proportion of students that want to go to the zoo is not 85%.
Example 7
Suppose a consumer group suspects that the proportion of households that have three cell phones is 30%. A cell phone company survey 150 households with the result that 43 of the households have three cell phones. They believe that the proportion is less than 30%. Conduct a hypothesis test to check their claim at 5% significance level.
Show Answer
Ha : p < 0.3
5% significance level means [latex]\alpha[/latex] = 0.05.
= P ( [latex]\overline{p}[/latex] < 0.30)
= P ( [latex]\frac{\overline{p} - p}{\sqrt{\frac{pq}{n}}}[/latex] < [latex]\frac{\frac{43}{150} - 0.30}{\sqrt{\frac{(0.3)(0.7)}{150}}}[/latex] )
= P ( Z < – 0.3563)
Try It
Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p-value, state your conclusion, and identify the Type I and Type II errors.
Click here to show solution:
H0: p = 0.92
Ha: p < 0.92
p-value = 0.0046
Because p-value < 0.05, we reject the null hypothesis.
There is sufficient evidence to conclude that fewer than 92% of American adults own cell phones.
Type I Error: To conclude that fewer than 92% of American adults own cell phones when, in fact, 92% of American adults do own cell phones (reject the null hypothesis when the null hypothesis is true).
Type II Error: To conclude that 92% of American adults own cell phones when, in fact, fewer than 92% of American adults own cell phones (do not reject the null hypothesis when the null hypothesis is false).
Example 8
The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass. (Assume the population is normal. )
1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98 1.02; .95; .95
Is there convincing evidence that the average conductivity of this type of glass is greater than 1?
Use a significance level of 0.05.
Step-by-step Solution:
Significance level is 5% ([latex]\alpha[/latex] = 0.05)
= 0.0359
Since p-value < significance level, we reject null hypothesis.
Using TI-Calculator to solve:
Significance level is 5% ([latex]\alpha[/latex] = 0.05)
We will input the sample data into the TI-83 as follows.
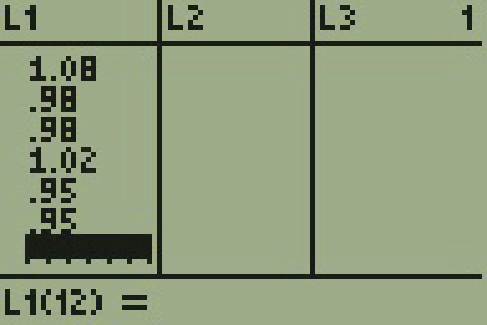
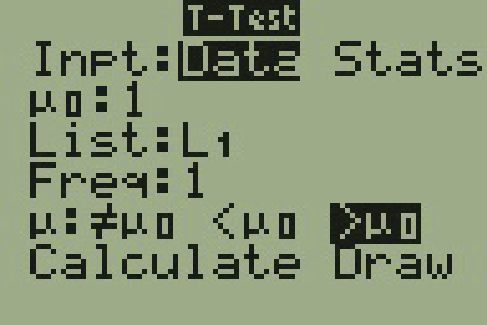
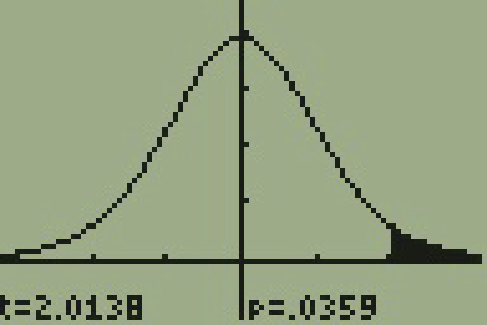
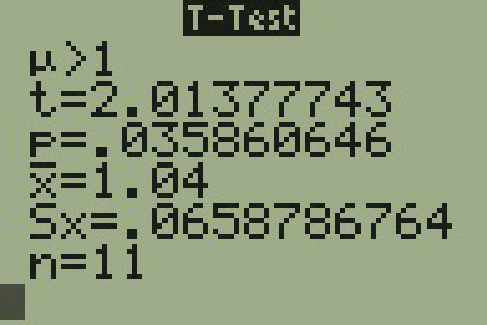
p-value = 0.03586
Since p-value < significance level, we reject null hypothesis.
Try It
In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). (Since this is a critical issue, use a 0.5% significance level to run the hypothesis test.
Step-by-step solution:
Significance level is 0.5% ([latex]\alpha[/latex] = 0.005)
= 0.00728
Since p-value < significance level, we reject null hypothesis.
Using TI-Calculator to solve:
Significance level is 0.5% ([latex]\alpha[/latex] = 0.005)

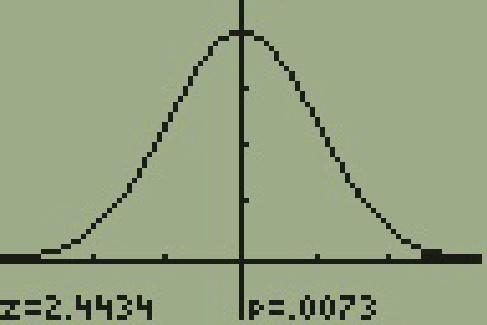
p-value = 0.00728
Since p-value < significance level, we reject null hypothesis.
We have sufficient evidence to conclude that cell phone users developed brain cancer at a greater rate.
Example 9
According to the US Census there are approximately 268,608,618 residents aged 12 and older. Statistics from the Rape, Abuse, and Incest National Network indicate that, on average, 207,754 rapes occur each year (male and female) for persons aged 12 and older. This translates into a percentage of sexual assaults of 0.07734%. In Daviess County, KY, there were reported 11 rapes for a population of 37,937. Conduct an appropriate hypothesis test to determine if there is a statistically significant difference between the local sexual assault percentage and the national sexual assault percentage. Use 1% significance level.
Show Answer
Significance level is 1% ([latex]\alpha[/latex] = 0.001)
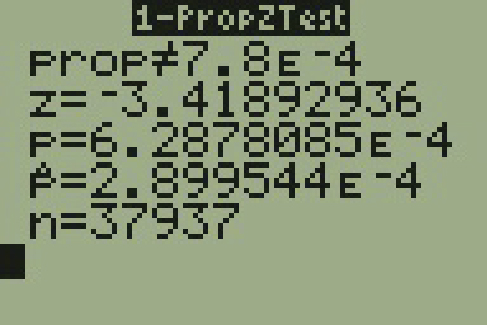
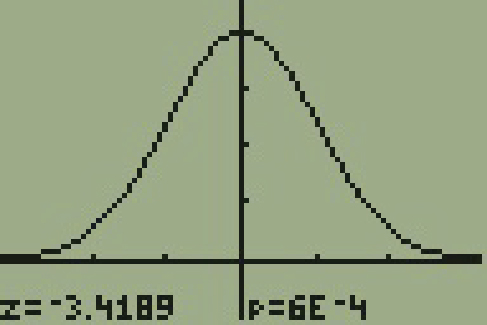
p-value = 0.0006288
Since p-value < significance level, we reject null hypothesis.
Concept Review
The hypothesis test itself has an established process. This can be summarized as follows:
Notice that in performing the hypothesis test, you use α and not β. β is needed to help determine the sample size of the data that is used in calculating the p-value. Remember that the quantity 1 – β is called thePower of the Test. A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

