131 Identify vertical and horizontal asymptotes

By looking at the graph of a rational function, we can investigate its local behavior and easily see whether there are asymptotes. We may even be able to approximate their location. Even without the graph, however, we can still determine whether a given rational function has any asymptotes, and calculate their location.

Vertical Asymptotes

The vertical asymptotes of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. Vertical asymptotes occur at the zeros of such factors.

How To: Given a rational function, identify any vertical asymptotes of its graph.

1. Factor the numerator and denominator.
2. Note any restrictions in the domain of the function.
3. Reduce the expression by canceling common factors in the numerator and the denominator.
4. Note any values that cause the denominator to be zero in this simplified version. These are where the vertical asymptotes occur.
5. Note any restrictions in the domain where asymptotes do not occur. These are removable discontinuities.

Example 5: Identifying Vertical Asymptotes

Find the vertical asymptotes of the graph of $k\left(x\right)=\frac{5+2x^2}{2-x-x^2}$.

Solution

First, factor the numerator and denominator.

$\{\begin{array}{l}k\left(x\right)=\frac{5+2x^2}{2-x-x^2}\\ =\frac{5+2x^2}{(2+x)(1-x)}\end{array}$

To find the vertical asymptotes, we determine where this function will be undefined by setting the denominator equal to zero:

$\{\begin{array}{l}(2+x)(1-x)=0\\ x=-2,1\end{array}$

Neither $x=-2$ nor $x=1$ are zeros of the numerator, so the two values indicate two vertical asymptotes. Figure 9 confirms the location of the two vertical asymptotes.

Removable Discontinuities

Occasionally, a graph will contain a hole: a single point where the graph is not defined, indicated by an open circle. We call such a hole a removable discontinuity.

For example, the function $f\left(x\right)=\frac{x^2-1}{x^2-2x-3}$ may be re-written by factoring the numerator and the denominator.

$f\left(x\right)=\frac{(x+1)(x-1)}{(x+1)(x-3)}$

Notice that $x+1$ is a common factor to the numerator and the denominator. The zero of this factor, $x=-1$, is the location of the removable discontinuity. Notice also that $x-3$ is not a factor in both the numerator and denominator. The zero of this factor, $x=3$, is the vertical asymptote.

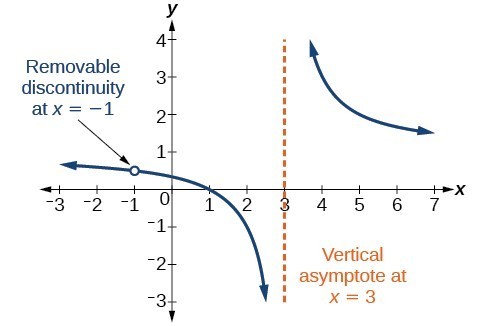
A General Note: Removable Discontinuities of Rational Functions

A removable discontinuity occurs in the graph of a rational function at $x=a$ if a is a zero for a factor in the denominator that is common with a factor in the numerator. We factor the numerator and denominator and check for common factors. If we find any, we set the common factor equal to 0 and solve. This is the location of the removable discontinuity. This is true if the multiplicity of this factor is greater than or equal to that in the denominator. If the multiplicity of this factor is greater in the denominator, then there is still an asymptote at that value.

Example 6: Identifying Vertical Asymptotes and Removable Discontinuities for a Graph

Find the vertical asymptotes and removable discontinuities of the graph of $k\left(x\right)=\frac{x-2}{x^2-4}$.

Solution

Factor the numerator and the denominator.

$k\left(x\right)=\frac{x-2}{(x-2)(x+2)}$

Notice that there is a common factor in the numerator and the denominator, $x-2$. The zero for this factor is $x=2$. This is the location of the removable discontinuity.

Notice that there is a factor in the denominator that is not in the numerator, $x+2$. The zero for this factor is $x=-2$. The vertical asymptote is $x=-2$.

The graph of this function will have the vertical asymptote at $x=-2$, but at $x=2$ the graph will have a hole.

Try It 5

Find the vertical asymptotes and removable discontinuities of the graph of $f\left(x\right)=\frac{x^2-25}{x^3-6x^2+5x}$.

Solution

Horizontal asymptotes

While vertical asymptotes describe the behavior of a graph as the output gets very large or very small, horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Recall that a polynomial’s end behavior will mirror that of the leading term. Likewise, a rational function’s end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions.

There are three distinct outcomes when checking for horizontal asymptotes:

Case 1: If the degree of the denominator > degree of the numerator, there is a horizontal asymptote at y = 0.

In this case, the end behavior is $f\left(x\right)\approx \frac{4x}{x^2}=\frac{4}{x}$. This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function $g\left(x\right)=\frac{4}{x}$, and the outputs will approach zero, resulting in a horizontal asymptote at y = 0. Note that this graph crosses the horizontal asymptote.

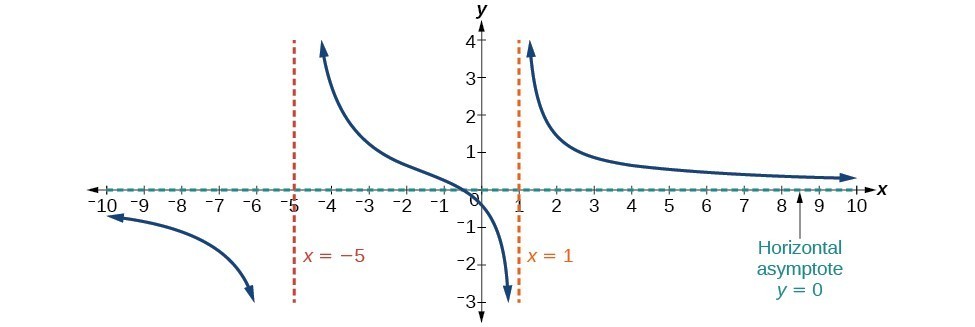
Figure 12. Horizontal Asymptote y = 0 when $f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0\text{ where degree of }p<\text{degree of q}$.

Case 2: If the degree of the denominator < degree of the numerator by one, we get a slant asymptote.

In this case, the end behavior is $f\left(x\right)\approx \frac{3x^2}{x}=3x$. This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function $g\left(x\right)=3x$. As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. However, the graph of $g\left(x\right)=3x$ looks like a diagonal line, and since f will behave similarly to g, it will approach a line close to $y=3x$. This line is a slant asymptote.

To find the equation of the slant asymptote, divide $\frac{3x^2-2x+1}{x-1}$. The quotient is $3x+1$, and the remainder is 2. The slant asymptote is the graph of the line $g\left(x\right)=3x+1$.

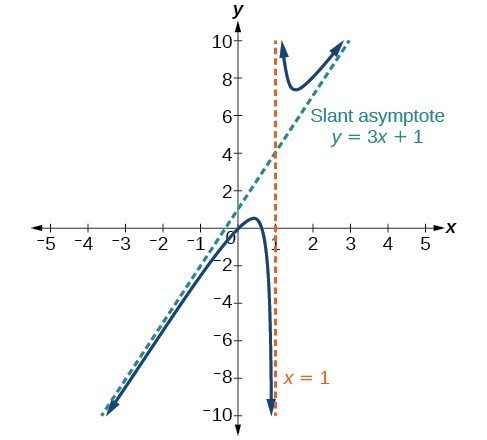
Figure 13. Slant Asymptote when $f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0$ where degree of $p>\text{ degree of }q\text{ by }1$.

Case 3: If the degree of the denominator = degree of the numerator, there is a horizontal asymptote at $y=\frac{a_n}{b_n}$, where $a_n$ and $b_n$ are the leading coefficients of $p\left(x\right)$ and $q\left(x\right)$ for $f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0$.

In this case, the end behavior is $f\left(x\right)\approx \frac{3x^2}{x^2}=3$. This tells us that as the inputs grow large, this function will behave like the function $g\left(x\right)=3$, which is a horizontal line. As $x\to \pm \mathrm{\infty },f\left(x\right)\to 3$, resulting in a horizontal asymptote at y = 3. Note that this graph crosses the horizontal asymptote.

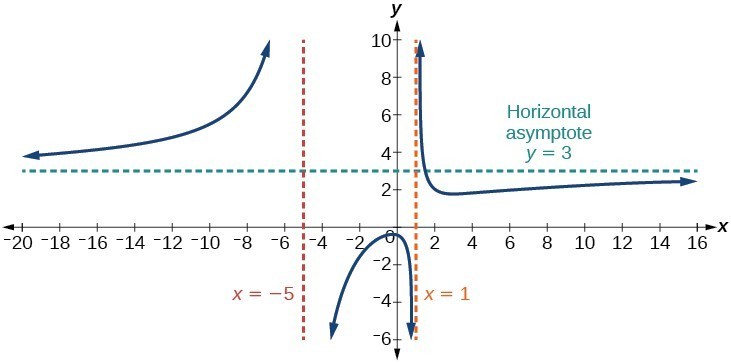
Figure 14. Horizontal Asymptote when $f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0\text{where degree of }p=\text{degree of }q$.

Notice that, while the graph of a rational function will never cross a vertical asymptote, the graph may or may not cross a horizontal or slant asymptote. Also, although the graph of a rational function may have many vertical asymptotes, the graph will have at most one horizontal (or slant) asymptote.

It should be noted that, if the degree of the numerator is larger than the degree of the denominator by more than one, the end behavior of the graph will mimic the behavior of the reduced end behavior fraction. For instance, if we had the function

with end behavior

the end behavior of the graph would look similar to that of an even polynomial with a positive leading coefficient.

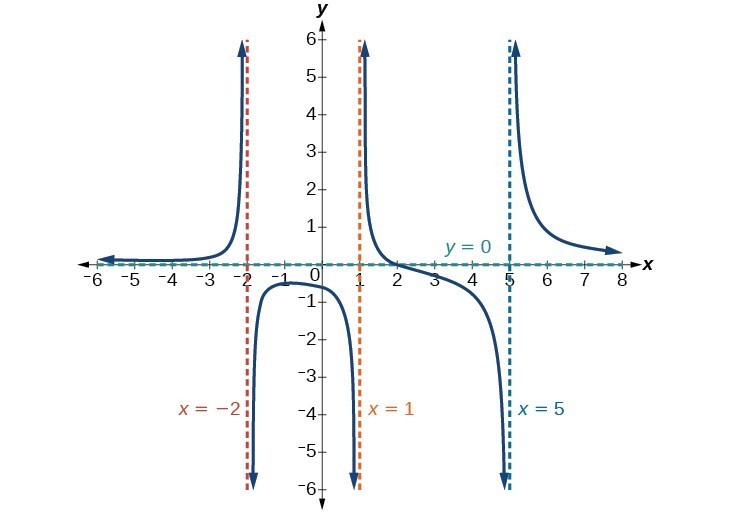
Example 9: Identifying Horizontal and Vertical Asymptotes

Find the horizontal and vertical asymptotes of the function

$f\left(x\right)=\frac{(x-2)(x+3)}{(x-1)(x+2)(x-5)}$

Solution

First, note that this function has no common factors, so there are no potential removable discontinuities.

The function will have vertical asymptotes when the denominator is zero, causing the function to be undefined. The denominator will be zero at $x=1,-2,\text{and }5$, indicating vertical asymptotes at these values.

The numerator has degree 2, while the denominator has degree 3. Since the degree of the denominator is greater than the degree of the numerator, the denominator will grow faster than the numerator, causing the outputs to tend towards zero as the inputs get large, and so as $x\to \pm \mathrm{\infty },f\left(x\right)\to 0$. This function will have a horizontal asymptote at $y=0$.

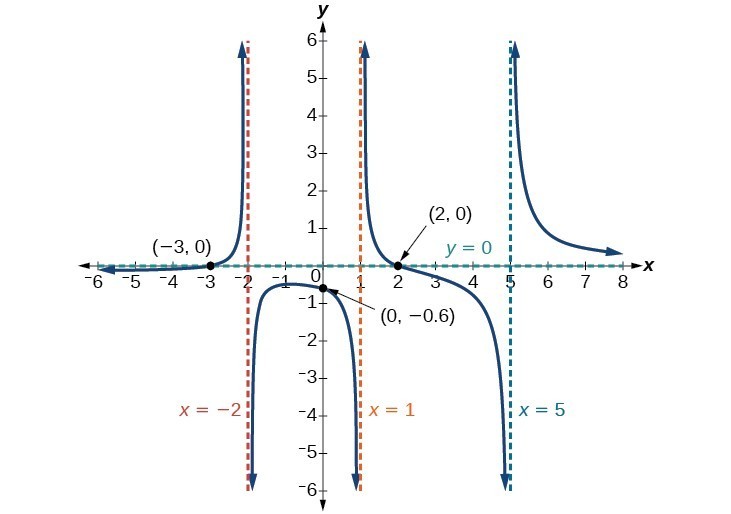
Example 10: Finding the Intercepts of a Rational Function

Find the intercepts of $f\left(x\right)=\frac{(x-2)(x+3)}{(x-1)(x+2)(x-5)}$.

Solution

We can find the y-intercept by evaluating the function at zero

$\{\begin{array}{l}f\left(0\right)=\frac{(0-2)(0+3)}{(0-1)(0+2)(0-5)}\\ =\frac{-6}{10}\\ =-\frac{3}{5}\\ =-0.6\end{array}$

The x-intercepts will occur when the function is equal to zero:

$\{\begin{array}{ll}0=\frac{(x-2)(x+3)}{(x-1)(x+2)(x-5)}& \text{This is zero when the numerator is zero}.\\ 0=(x-2)(x+3)& \hfill \hfill \\ x=2,-3& \hfill \hfill \end{array}$

The y-intercept is $(0,-0.6)$, the x-intercepts are $(2,0)$ and $(-3,0)$.