83 Solve an absolute value equation
Now that we can graph an absolute value function, we will learn how to solve an absolute value equation. To solve an equation such as [latex]{8}=\left|{2}x - {6}\right|\\[/latex], we notice that the absolute value will be equal to 8 if the quantity inside the absolute value is 8 or -8. This leads to two different equations we can solve independently.
Knowing how to solve problems involving absolute value functions is useful. For example, we may need to identify numbers or points on a line that are at a specified distance from a given reference point.
An absolute value equation is an equation in which the unknown variable appears in absolute value bars. For example,
A General Note: Solutions to Absolute Value Equations
For real numbers [latex]A\\[/latex] and [latex]B\\[/latex], an equation of the form [latex]|A|=B\\[/latex], with [latex]B\ge 0\\[/latex], will have solutions when [latex]A=B\\[/latex] or [latex]A=-B\\[/latex]. If [latex]B<0\\[/latex], the equation [latex]|A|=B\\[/latex] has no solution.
How To: Given the formula for an absolute value function, find the horizontal intercepts of its graph.
- Isolate the absolute value term.
- Use [latex]|A|=B\\[/latex] to write [latex]A=B\\[/latex] or [latex]\mathrm{-A}=B\\[/latex], assuming [latex]B>0\\[/latex].
- Solve for [latex]x\\[/latex].
Example 4: Finding the Zeros of an Absolute Value Function
For the function [latex]f\left(x\right)=|4x+1|-7\\[/latex] , find the values of [latex]x\\[/latex] such that [latex]\text{ }f\left(x\right)=0\\[/latex] .
Solution
[latex]\begin{cases}0=|4x+1|-7\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \text{Substitute 0 for }f\left(x\right).\hfill \\ 7=|4x+1|\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \text{Isolate the absolute value on one side of the equation}.\hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ 7=4x+1\hfill & \text{or}\hfill & \hfill & \hfill & \hfill & -7=4x+1\hfill & \text{Break into two separate equations and solve}.\hfill \\ 6=4x\hfill & \hfill & \hfill & \hfill & \hfill & -8=4x\hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ x=\frac{6}{4}=1.5\hfill & \hfill & \hfill & \hfill & \hfill & \text{ }x=\frac{-8}{4}=-2\hfill & \hfill \end{cases}\\[/latex]

The function outputs 0 when [latex]x=1.5[/latex] or [latex]x=-2\\[/latex].
Try It 4
For the function [latex]f\left(x\right)=|2x - 1|-3\\[/latex], find the values of [latex]x\\[/latex] such that [latex]f\left(x\right)=0\\[/latex].
Q & A
Should we always expect two answers when solving [latex]|A|=B?\\[/latex]
No. We may find one, two, or even no answers. For example, there is no solution to [latex]2+|3x - 5|=1\\[/latex].
How To: Given an absolute value equation, solve it.
- Isolate the absolute value term.
- Use [latex]|A|=B\\[/latex] to write [latex]A=B\\[/latex] or [latex]A=\mathrm{-B}\\[/latex].
- Solve for [latex]x\\[/latex].
Example 5: Solving an Absolute Value Equation
Solve [latex]1=4|x - 2|+2\\[/latex].
Solution
Isolating the absolute value on one side of the equation gives the following.
The absolute value always returns a positive value, so it is impossible for the absolute value to equal a negative value. At this point, we notice that this equation has no solutions.
Q & A
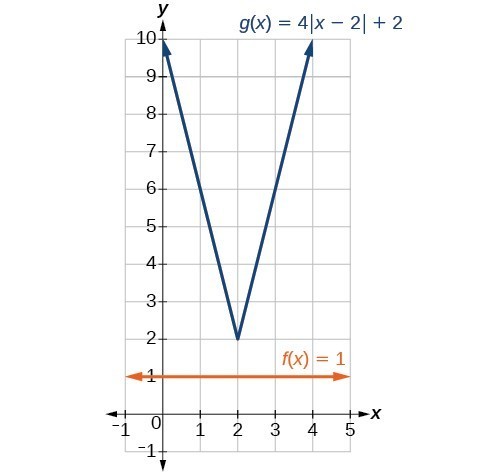
In Example 5, if [latex]f\left(x\right)=1\\[/latex] and [latex]g\left(x\right)=4|x - 2|+2\\[/latex] were graphed on the same set of axes, would the graphs intersect?
No. The graphs of [latex]f\\[/latex] and [latex]g\\[/latex] would not intersect. This confirms, graphically, that the equation [latex]1=4|x - 2|+2\\[/latex] has no solution.
Try It 5
Find where the graph of the function [latex]f\left(x\right)=-|x+2|+3\\[/latex] intersects the horizontal and vertical axes.

