225 Reading: Game Theory

The Prisoners’ Dilemma

Suppose a local district attorney (DA) is certain that two individuals, Frankie and Johnny, have committed a burglary, but she has no evidence that would be admissible in court.

The DA arrests the two. On being searched, each is discovered to have a small amount of cocaine. The DA now has a sure conviction on a possession of cocaine charge, but she will get a conviction on the burglary charge only if at least one of the prisoners confesses and implicates the other.

The DA decides on a strategy designed to elicit confessions. She separates the two prisoners and then offers each the following deal: “If you confess and your partner doesn’t, you will get the minimum sentence of one year in jail on the possession and burglary charges. If you both confess, your sentence will be three years in jail. If your partner confesses and you do not, the plea bargain is off and you will get six years in prison. If neither of you confesses, you will each get two years in prison on the drug charge.”

The two prisoners each face a dilemma; they can choose to confess or not confess. Because the prisoners are separated, they cannot plot a joint strategy. Each must make a strategic choice in isolation.

The outcomes of these strategic choices, as outlined by the DA, depend on the strategic choice made by the other prisoner. The payoff matrix for this game is given in Figure 11.6 “Payoff Matrix for the Prisoners’ Dilemma”. The two rows represent Frankie’s strategic choices; she may confess or not confess. The two columns represent Johnny’s strategic choices; he may confess or not confess. There are four possible outcomes: Frankie and Johnny both confess (cell A), Frankie confesses but Johnny does not (cell B), Frankie does not confess but Johnny does (cell C), and neither Frankie nor Johnny confesses (cell D). The portion at the lower left in each cell shows Frankie’s payoff; the shaded portion at the upper right shows Johnny’s payoff.

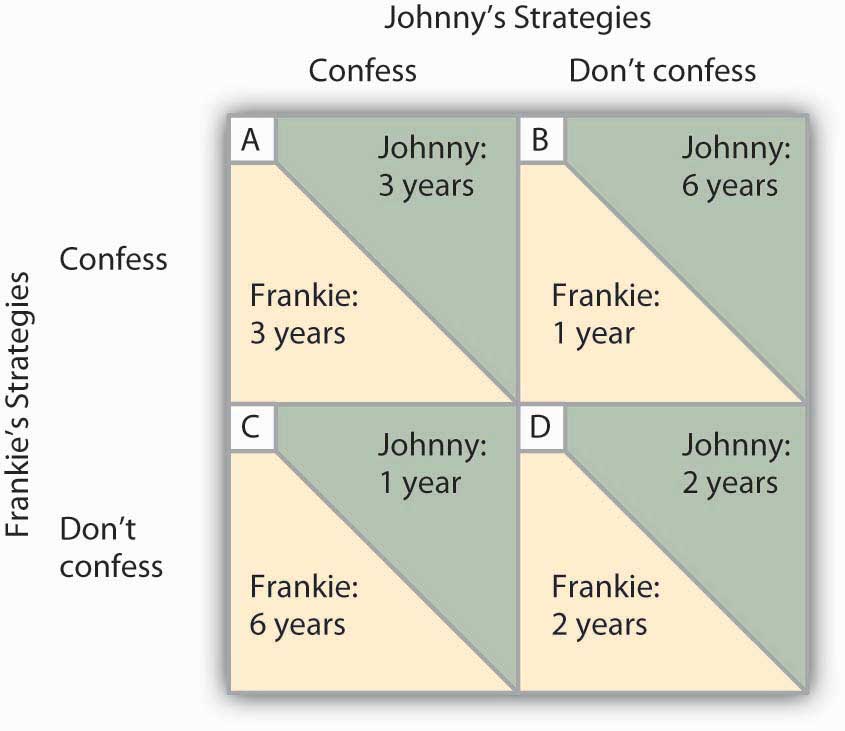
If Johnny confesses, Frankie’s best choice is to confess—she will get a three-year sentence rather than the six-year sentence she would get if she did not confess. If Johnny does not confess, Frankie’s best strategy is still to confess—she will get a one-year rather than a two-year sentence. In this game, Frankie’s best strategy is to confess, regardless of what Johnny does. When a player’s best strategy is the same regardless of the action of the other player, that strategy is said to be a dominant strategy. Frankie’s dominant strategy is to confess to the burglary.

For Johnny, the best strategy to follow, if Frankie confesses, is to confess. The best strategy to follow if Frankie does not confess is also to confess. Confessing is a dominant strategy for Johnny as well. A game in which there is a dominant strategy for each player is called a dominant strategy equilibrium. Here, the dominant strategy equilibrium is for both prisoners to confess; the payoff will be given by cell A in the payoff matrix.

From the point of view of the two prisoners together, a payoff in cell D would have been preferable. Had they both denied participation in the robbery, their combined sentence would have been four years in prison—two years each. Indeed, cell D offers the lowest combined prison time of any of the outcomes in the payoff matrix. But because the prisoners cannot communicate, each is likely to make a strategic choice that results in a more costly outcome. Of course, the outcome of the game depends on the way the payoff matrix is structured.

Repeated Oligopoly Games

The prisoners’ dilemma was played once, by two players. The players were given a payoff matrix; each could make one choice, and the game ended after the first round of choices.

The real world of oligopoly has as many players as there are firms in the industry. They play round after round: a firm raises its price, another firm introduces a new product, the first firm cuts its price, a third firm introduces a new marketing strategy, and so on. An oligopoly game is a bit like a baseball game with an unlimited number of innings—one firm may come out ahead after one round, but another will emerge on top another day. In the computer industry game, the introduction of personal computers changed the rules. IBM, which had won the mainframe game quite handily, struggles to keep up in a world in which rivals continue to slash prices and improve quality.

Oligopoly games may have more than two players, so the games are more complex, but this does not change their basic structure. The fact that the games are repeated introduces new strategic considerations. A player must consider not just the ways in which its choices will affect its rivals now, but how its choices will affect them in the future as well.

We will keep the game simple, however, and consider a duopoly game. The two firms have colluded, either tacitly or overtly, to create a monopoly solution. As long as each player upholds the agreement, the two firms will earn the maximum economic profit possible in the enterprise.

There will, however, be a powerful incentive for each firm to cheat. The monopoly solution may generate the maximum economic profit possible for the two firms combined, but what if one firm captures some of the other firm’s profit? Suppose, for example, that two equipment rental firms, Quick Rent and Speedy Rent, operate in a community. Given the economies of scale in the business and the size of the community, it is not likely that another firm will enter. Each firm has about half the market, and they have agreed to charge the prices that would be chosen if the two combined as a single firm. Each earns economic profits of $20,000 per month.

Quick and Speedy could cheat on their arrangement in several ways. One of the firms could slash prices, introduce a new line of rental products, or launch an advertising blitz. This approach would not be likely to increase the total profitability of the two firms, but if one firm could take the other by surprise, it might profit at the expense of its rival, at least for a while.

We will focus on the strategy of cutting prices, which we will call a strategy of cheating on the duopoly agreement. The alternative is not to cheat on the agreement. Cheating increases a firm’s profits if its rival does not respond. Figure 11.7 “To Cheat or Not to Cheat: Game Theory in Oligopoly” shows the payoff matrix facing the two firms at a particular time. As in the prisoners’ dilemma matrix, the four cells list the payoffs for the two firms. If neither firm cheats (cell D), profits remain unchanged.

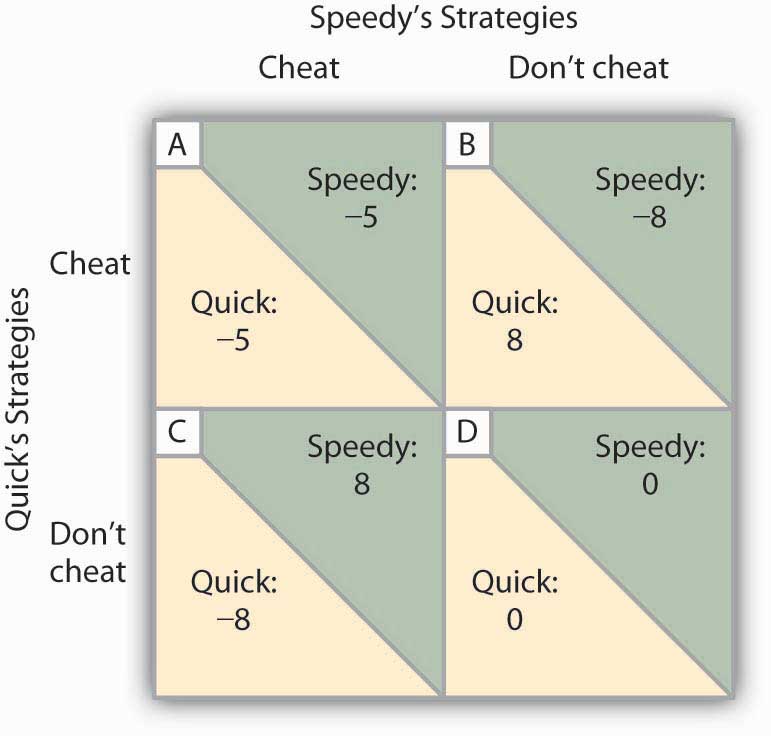
Two rental firms, Quick Rent and Speedy Rent, operate in a duopoly market. They have colluded in the past, achieving a monopoly solution. Cutting prices means cheating on the arrangement; not cheating means maintaining current prices. The payoffs are changes in monthly profits, in thousands of dollars. If neither firm cheats, then neither firm’s profits will change. In this game, cheating is a dominant strategy equilibrium.

This game has a dominant strategy equilibrium. Quick’s preferred strategy, regardless of what Speedy does, is to cheat. Speedy’s best strategy, regardless of what Quick does, is to cheat. The result is that the two firms will select a strategy that lowers their combined profits!

Quick Rent and Speedy Rent face an unpleasant dilemma. They want to maximize profit, yet each is likely to choose a strategy inconsistent with that goal. If they continue the game as it now exists, each will continue to cut prices, eventually driving prices down to the point where price equals average total cost (presumably, the price-cutting will stop there). But that would leave the two firms with zero economic profits.

Both firms have an interest in maintaining the status quo of their collusive agreement. Overt collusion is one device through which the monopoly outcome may be maintained, but that is illegal. One way for the firms to encourage each other not to cheat is to use a tit-for-tat strategy. In a tit-for-tat strategy a firm responds to cheating by cheating, and it responds to cooperative behavior by cooperating. As each firm learns that its rival will respond to cheating by cheating, and to cooperation by cooperating, cheating on agreements becomes less and less likely.

Still another way firms may seek to force rivals to behave cooperatively rather than competitively is to use a trigger strategy, in which a firm makes clear that it is willing and able to respond to cheating by permanently revoking an agreement. A firm might, for example, make a credible threat to cut prices down to the level of average total cost—and leave them there—in response to any price-cutting by a rival. A trigger strategy is calculated to impose huge costs on any firm that cheats—and on the firm that threatens to invoke the trigger. A firm might threaten to invoke a trigger in hopes that the threat will forestall any cheating by its rivals.

Game theory has proved to be an enormously fruitful approach to the analysis of a wide range of problems. Corporations use it to map out strategies and to anticipate rivals’ responses. Governments use it in developing foreign-policy strategies. Military leaders play war games on computers using the basic ideas of game theory. Any situation in which rivals make strategic choices to which competitors will respond can be assessed using game theory analysis.

One rather chilly application of game theory analysis can be found in the period of the Cold War when the United States and the former Soviet Union maintained a nuclear weapons policy that was described by the acronym MAD, which stood for mutually assured destruction. Both countries had enough nuclear weapons to destroy the other several times over, and each threatened to launch sufficient nuclear weapons to destroy the other country if the other country launched a nuclear attack against it or any of its allies. On its face, the MAD doctrine seems, well, mad. It was, after all, a commitment by each nation to respond to any nuclear attack with a counterattack that many scientists expected would end human life on earth. As crazy as it seemed, however, it worked. For 40 years, the two nations did not go to war. While the collapse of the Soviet Union in 1991 ended the need for a MAD doctrine, during the time that the two countries were rivals, MAD was a very effective trigger indeed.

Of course, the ending of the Cold War has not produced the ending of a nuclear threat. Several nations now have nuclear weapons. The threat that Iran will introduce nuclear weapons, given its stated commitment to destroy the state of Israel, suggests that the possibility of nuclear war still haunts the world community.

Self Check: Game Theory

Answer the question(s) below to see how well you understand the topics covered in the previous section. This short quiz does not count toward your grade in the class, and you can retake it an unlimited number of times.

You’ll have more success on the Self Check if you’ve completed the two Readings in this section.

Use this quiz to check your understanding and decide whether to (1) study the previous section further or (2) move on to the next section.